Нужна ! ребро куба равно а. вычислите периметр и площадь сечения, проходящего через концы трёх рёбер, выходящих из вершины куба.
Ответы
Если я правильно поняла, сечение будет в виде равностороннего треугольника стороны которого будут равны диагонали грани (квадрата). Диагональ равна: 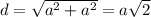 Периметр:
Периметр: 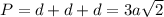 Площадь сечения (треугольника) найдём через высоту:
Площадь сечения (треугольника) найдём через высоту: 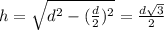
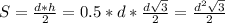 Заменим d на a:
Заменим d на a: 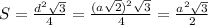
ПОКАЗАТЬ ОТВЕТЫ
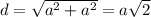 Периметр:
Периметр: 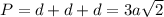 Площадь сечения (треугольника) найдём через высоту:
Площадь сечения (треугольника) найдём через высоту: 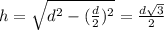
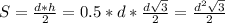 Заменим d на a:
Заменим d на a: 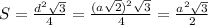
Другие вопросы по теме Геометрия
Популярные вопросы
- Вкакой строке числа расположены в порядке возрастания а)435см,436м,437дм б)564мм,563см,562дм...
3 - Отгадайте слово по его лексическому значению. какие объяснения слова используются...
1 - Три з єднані в електриче коло , таким чином , що 2-ий і 3-ий з єднані паралельно...
3 - Прочитайте соблюдая правильную интонацию перепишиье рамставляя знаки препинания...
1 - Сколько корней имеет уравнение: (cosx-sinx)^2=1-2sin2x на отрезке [20пи/9; 28пи/9]...
1 - Сложные прилагательные черты человека внешнасть...
1 - Ii. переведите предложения и укажите временную форму по модели: образец: she...
2 - Вставьте пропущенные слова, чтобы получились верные высказывания. славянскую...
1 - 96÷16=6.напишите подробно (в действиях), как получили 6. это третий класс....
1 - Iii. сделайте из активной формы пассивную по модели. переведите пассивную форму....
2