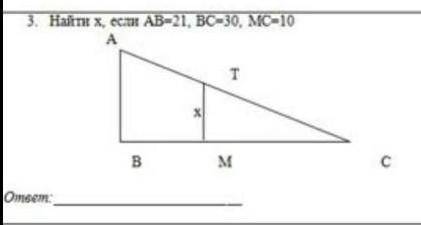
Найти x, если AB=21, BC = 30, MC = 10

Дано

АB=21 см

BC=30 см

МС=10 см

Найти

Х-?

АВ/ТМ=АС/ТС=ВС/МС = 21/х= 30/10

30х=210

х=7

Для решения этой задачи мы можем использовать теорему Пифагора. Теорема Пифагора гласит, что в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов. В данной задаче треугольник АВС не является прямоугольным, поэтому нам понадобится построить высоту из вершины В к гипотенузе AC.

1. Начнем с построения высоты. Обозначим точку пересечения высоты и гипотенузы как М.

Заметим, что треугольник AMB прямоугольный, поскольку AM является высотой. Также треугольник BMC прямоугольный, поскольку BM является высотой.

2. Используя теорему Пифагора для треугольника AMB, можем записать уравнение:

AB^2 = AM^2 + MB^2.

Заменяем значения:

21^2 = AM^2 + x^2.

3. Используя теорему Пифагора для треугольника BMC, можем записать уравнение:

BC^2 = BM^2 + CM^2.

Заменяем значения:

30^2 = x^2 + 10^2.

4. Теперь у нас есть система из двух уравнений:

21^2 = AM^2 + x^2,
30^2 = x^2 + 10^2.

5. Решим систему уравнений для нахождения значения х.

Первое уравнение можно переписать в виде:

AM^2 = 21^2 - x^2.

Подставляем это значение во второе уравнение:

30^2 = x^2 + 10^2,

900 = 21^2 - x^2 + 100.

Упрощаем:

x^2 = 441 - 100 + 900 - 441.

x^2 = 900 - 441 - 100 + 441.

x^2 = 900 - 100.

x^2 = 800.

6. Чтобы найти значение х, найдем квадратный корень из обеих сторон уравнения:

x = √800.

7. Подсчитаем значение корня из 800:

x ≈ 28,284.

Ответ: x ≈ 28,284.

Таким образом, x равно примерно 28,284.