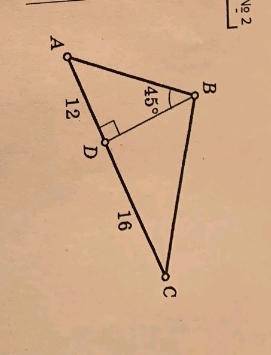
Найти S∆ abc ad-12см dc-16см угол b 45

Для решения данной задачи нам понадобятся знания о площади треугольника и тригонометрии.

1. Сначала найдем площадь треугольника ABC. Для этого воспользуемся формулой S = 1/2 * a * h, где a - основание треугольника, h - высота, проведенная к этому основанию.

В данном случае основание треугольника ABC - отрезок AB, который равен длине отрезка AD, то есть 12 см.
Высота треугольника ABC - отрезок DC, который равен 16 см.

Подставим значения в формулу:
SABC = 1/2 * 12 см * 16 см = 96 см²

Итак, площадь треугольника ABC равна 96 см².

2. Далее нам нужно найти площадь треугольника ADB. Здесь мы не знаем высоту треугольника, но знаем длины его сторон и угла между ними.

Для нахождения площади треугольника по сторонам и углу между ними воспользуемся формулой S = 1/2 * a * b * sin(C), где a и b - длины сторон треугольника, C - угол между этими сторонами.

В данном случае стороны треугольника ADB равны AD (12 см) и BD (не указано в задаче), а угол между ними - угол B (45°).

Вычислим площадь треугольника ADB:
SADB = 1/2 * 12 см * BD * sin(45°)

Теперь нам нужно найти длину стороны BD. Для этого воспользуемся теоремой Пифагора, так как треугольник ABD - прямоугольный треугольник.

Из рисунка видно, что сторона AB параллельна стороне CD, поэтому треугольники ABC и ADB подобны. Это означает, что отношение длин соответствующих сторон этих треугольников равно.

Поэтому можно записать следующее:

AB/AD = AC/DC
AB/AD = BC/DC
AB/12 = 16/DC

Переставим формулу:
DC = 16*12/AB

Вспомним, что треугольник ABC - равнобедренный треугольник, так как две его стороны (AB и BC) равны.
Если треугольник ABC равнобедренный, то AC - медиана, которая проведена к основанию, равна половине основания.

Таким образом, AC = AB/2 = 12/2 = 6 см.

Подставим значения в формулу для нахождения DC:
DC = 16*12/6 = 32 см

Итак, сторона BD равна 32 см.

Вернемся к формуле для нахождения площади треугольника ADB и подставим значения:
SADB = 1/2 * 12 см * 32 см * sin(45°)

Для вычисления sin(45°) воспользуемся таблицей значений тригонометрической функции:
sin(45°) = √2/2 ≈ 0.707

Подставим значение в формулу:
SADB = 1/2 * 12 см * 32 см * 0.707 ≈ 169.89 см²

Итак, площадь треугольника ADB равна примерно 169.89 см².

3. Наконец, чтобы найти площадь треугольника ∆ABC∆ABC - ∆ADB∆ADB, нужно из площади треугольника ABC вычесть площадь треугольника ADB.

S∆ABC∆ADB = SABC - SADB
S∆ABC∆ADB = 96 см² - 169.89 см² ≈ -73.89 см²

Итак, площадь треугольника ∆ABC∆ABC - ∆ADB∆ADB равна примерно -73.89 см².

Окончательный ответ: S∆ABC∆ADB ≈ -73.89 см².