Найти радиус окружности, вписаной в равнобедренную трапецию, если ее большее основание равно а, а угол при меньшем основании 120 градусов.
Ответы
В трапецию можно вписать окружность когда сумма боковых сторона равна сумме оснований. Пусть основания равны 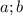 . Боковая сторона равна
. Боковая сторона равна 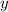 . Тогда
. Тогда
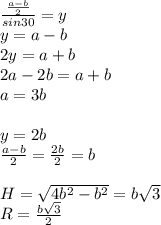
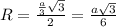
ПОКАЗАТЬ ОТВЕТЫ
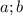 . Боковая сторона равна
. Боковая сторона равна 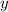 . Тогда
. Тогда 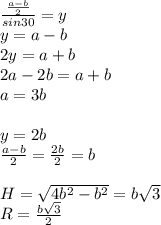
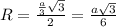
Другие вопросы по теме Геометрия
Популярные вопросы
- 1)стой за правду горой. 2)век живи, век учись. 3)дело словом не...
2 - Перевести из активного залога в пасcивный: 1 the usually visit...
1 - Напиши несколько предложений, исползуя эти словосочетание. время...
3 - Мне нужно сочинение муму сделайте чтобы были 8 красных строк...
1 - Треугольник abc равнобедренный, вd - медиана. докажите что 1 )...
1 - Как можно назвать владение двумя языками 1) лингвистика 2) билингвизм...
2 - Какими чертами должен обладать человек, чтобы его могли назвать...
2 - (6, 5*10)*(3, 8*10 4 )только сверху решите...
2 - Выражение 3 целых 3/5х + 4целых 10/21 + 1 целая 1/2х + 2 целых1/3...
3 - Религиозный состав восточной европы. (сколько стран? ) католицизм...
2