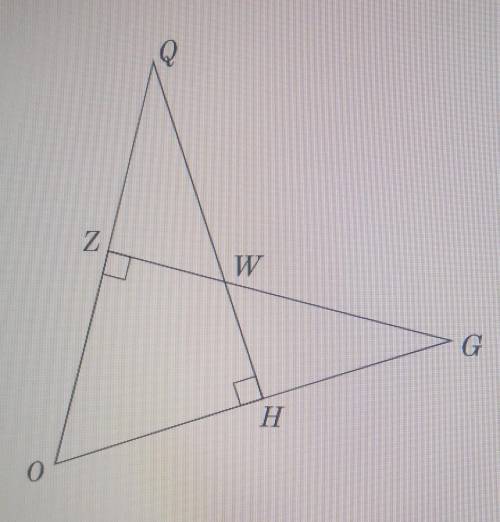
Найти QZ если GH=27,89 см а OZ=OH
Другие вопросы по теме Геометрия
Популярные вопросы
- Знайдить площу прямокутного трикутника и гипотенуза доривнюе 13 сантиметров...
3 - сдать сегодня!Даю 10б сдать сегодня!Даю 10б. >...
3 - Тело массой 100 г свободнo без начальной скорости падает с высоты 2,9 м...
2 - Про кого з князів літописець пише: “... кинувся був на поганих (язичників),...
3 - 1/2 * √2/2 * √3/2 * 1 дам :)...
2 - Англ мова зделайте Англ мова зделайте...
3 - Прочитайте текст і визначте назву штату США: Штат, який відіграє нині виняткову...
2 - 25. В селе Александровка 500 огородов. На 250 огородах растёт морковь,на...
1 - Допущено помилку у відмінюванні числівника варіанти відповідей п ятдесяти...
3 - с английским с английским >...
2
1. Рассмотрим треугольник GHQ. Мы знаем, что GH = 27,89 см. Для нахождения QZ нам нужно знать значение GQ.
2. Обратимся к треугольнику OGH. Мы знаем, что OZ = OH. Так как треугольник OGH является равнобедренным, то мы можем сделать вывод, что OG = OH.
3. Мы также знаем, что GH = 27,89 см. Отсюда следует, что OG = (GH / 2) = (27,89 / 2) = 13,945 см.
4. Вернемся к треугольнику GHQ. Мы уже знаем, что OG = 13,945 см. Так как GQ является медианой треугольника GHQ, то мы можем сделать вывод, что GQ = (2/3) * OG.
5. Вычислим значение GQ: GQ = (2/3) * 13,945 = 9,2967 см.
6. Теперь у нас есть значение GQ. Чтобы найти QZ, мы можем использовать теорему Пифагора для треугольника GHQ. Теорема Пифагора утверждает, что квадрат гипотенузы равен сумме квадратов катетов.
7. В нашем случае гипотенузой является GQ, а катетами являются GH и QZ. Используя теорему Пифагора, мы получаем уравнение: (GQ^2) = (GH^2) + (QZ^2).
8. Подставим значения GH = 27,89 и GQ = 9,2967 в уравнение и найдем QZ:
(9,2967^2) = (27,89^2) + (QZ^2)
86,54395 = 776,7521 + (QZ^2)
QZ^2 = 86,54395 - 776,7521
QZ^2 = -690,20815
9. У нас получается отрицательное значение для QZ^2, что не имеет смысла.
10. Итак, такое значение QZ невозможно найти в заданном треугольнике. Мы можем заключить, что треугольник GHQ не является прямоугольным.