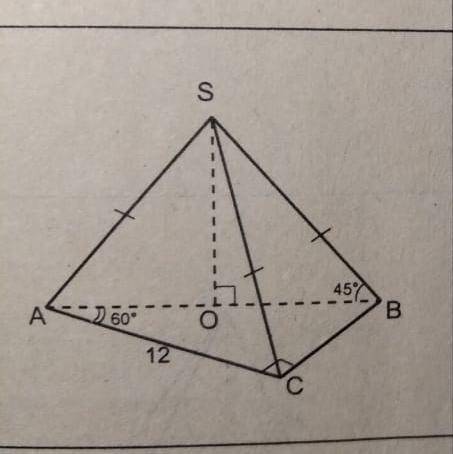
Найти полную поверхность пирамиды с чертежом и объяснением

Добрый день! Рад, что вы обратились ко мне за помощью. Давайте решим эту задачу вместе.

Для начала давайте разберемся, что такое полная поверхность пирамиды. Полная поверхность пирамиды - это сумма площадей всех ее боковых граней и площади основания.

У нас дан чертеж пирамиды, и чтобы найти полную поверхность, нам нужно вычислить площади каждой из ее граней.

Рассмотрим каждую грань пирамиды отдельно.

1. Положим, что сторона основания пирамиды равна a, а высота пирамиды равна h.
2. Для начала найдем площадь основания пирамиды. Основание пирамиды - это правильный треугольник, потому что все его стороны равны. Формула для вычисления площади треугольника - S = (a^2 * √3) / 4, где a - сторона треугольника.
В нашем случае, a = 8, поэтому площадь одного треугольника будет S = (8^2 * √3) / 4 = (64 * √3) / 4 = 16√3.

3. Теперь давайте найдем площадь каждой из боковых граней. Боковые грани пирамиды - это три равносторонних треугольника. Формула для вычисления площади равностороннего треугольника - S = (a^2 * √3) / 4.
В нашем случае, a = 8, поэтому площадь одного треугольника будет S = (8^2 * √3) / 4 = (64 * √3) / 4 = 16√3.

4. Так как боковых граней есть три, умножим площадь одной грани на три, чтобы получить площадь всех трех боковых граней. Отсюда, площадь всех трех боковых граней равна 3 * 16√3 = 48√3.

5. Наконец, найдем площадь полной поверхности пирамиды, сложив площадь основания и площадь всех трех боковых граней.
Площадь полной поверхности пирамиды = площадь основания + площадь всех боковых граней = 16√3 + 48√3 = 64√3.

Итак, полная поверхность пирамиды равна 64√3.

Вот, решение данной задачи. Если у вас остались вопросы или что-то непонятно, пожалуйста, скажите, и я с радостью помогу вам.