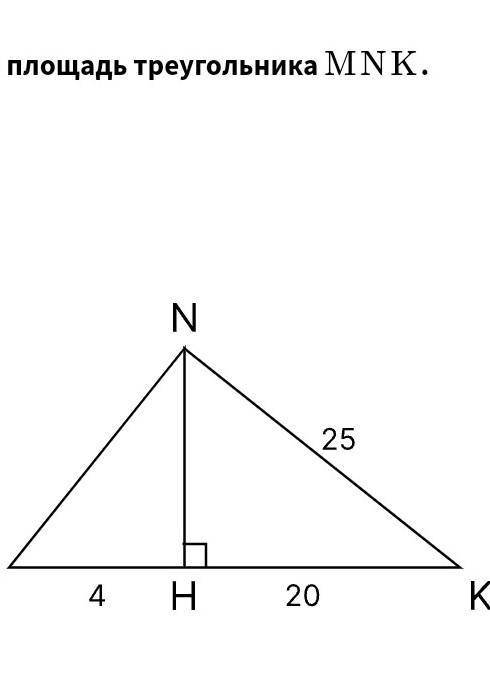
найти площадь треугольника

S=25•24=600 cm²

Объяснение:

S=a•b

Значит умножение ширины и длины или две стороны фигуры.

Для начала нужно заметить, что дан треугольник с заданными сторонами и углами.

Для нахождения площади треугольника, воспользуемся формулой полупериметра и герона, которая гласит: S = √(p * (p - a) * (p - b) * (p - c)), где S - площадь треугольника, а, b, c - длины сторон, p - полупериметр.

Шаг 1: Найдем полупериметр треугольника. Для этого нужно сложить длины всех сторон и поделить полученную сумму на 2:
p = (a + b + c) / 2,

где a, b, c - длины сторон треугольника.

Шаг 2: Подставим найденное значение полупериметра в формулу Герона:
S = √(p * (p - a) * (p - b) * (p - c)).

Шаг 3: Вычислим значение подкоренного выражения:
(p - a), (p - b) и (p - c).

Шаг 4: Подставим значения в формулу и выполним вычисления, чтобы найти площадь треугольника.

Предоставлю пример для данного треугольника:

Пусть a = 5, b = 7 и c = 8 (длины сторон треугольника).
Тогда полупериметр будет равен:
p = (5 + 7 + 8) / 2 = 20 / 2 = 10.

Подставим значения в формулу Герона:
S = √(10 * (10 - 5) * (10 - 7) * (10 - 8)).

Вычислим значение подкоренного выражения:
(10 - 5) = 5,
(10 - 7) = 3,
(10 - 8) = 2.

Теперь подставим значения в формулу:
S = √(10 * 5 * 3 * 2) = √(300) = 17.32.

Таким образом, площадь треугольника составляет приблизительно 17.32 квадратных единиц.

Надеюсь, ответ понятен и пошаговое решение помогло в понимании процесса нахождения площади треугольника.