Найти площадь сектора, ограниченной дугой окружности и стягивающей ее хордой, если длина хорды рана 8 под корнем 2 см, а градусная мера дуги равна 30 градусов
Другие вопросы по теме Геометрия
Популярные вопросы
- 1) чим відрізняється утворення вуглеводів у клітинах автотрофів ігетеротрофів?...
3 - Главные сражения полтавской битвы начинается в 9 часов утра 27 июня,...
3 - На пешите мне доклад по обж на тему вредные факторы, влияющие на...
1 - Определить электроемкость плоского конденсатора, площадь пластин...
2 - Найдите стороны равнобедренного треугольника если его периметр равен...
3 - Придумать пабудавальна апавядальны текст...
1 - 100 полное решение 1. трактор при движении саней по снегу может действовать...
1 - Найти массу 6х10^23 молекул амиака (nh3)...
1 - Разобраться с этим.принимаю только правильные ответы на вопросы....
2 - Умные люди я не понимаю , , я последние...
3
Сразу поправлю: часть круга, ограниченная дугой и её хордой называется сегментом.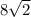 см)
см)
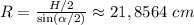
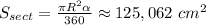
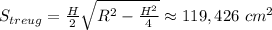
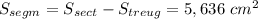
Его площадь равна площади сектора минус площадь треугольника AOB.
обозначения: точка O -центр круга; точки A, B -концы хорды
H -длина хорды (как я понял, равна
α -центральный угол AOB (для удобства в формулах)
Считать будем округлённо (если выразить ответ точно, то получится кучка дробей и радикалов).
В равнобедренном треугольнике AOB проведём высоту (пройдёт от точки O до центра хорды). Получим два прямоугольных треугольника- их гипотенуза равна радиусу круга, острый угол равен половине угла α. В прямоугольном треугольнике синус острого угла равен отношению противолежащего катета к гипотенузе. Используя это, выразим и найдём радиус:
Найдём площадь сектора:
Найдём площадь равнобедренного треугольника AOB по формуле:
И, наконец найдём площадь сегмента: