найти площадь прямоугольной трапеции , если радиус круга , вписаного в нее, равен 12 см , а тупой угол трапеции равен 150 градусам

Объяснение:

............ .......... . . ...

r=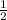 *h , откуда h = 24 см

острый угол трапеции равен 30° (360-90-90-150)

большая боковая сторона трапеции равна 48 см.

т.к. в трапецию вписана окружность, то по свойству суммы её боковых сторон и оснований равны.

сумма оснований = 24 см + 48 см = 72 см

Площадь трапеции =  1/2 * h * (a+b) =  1/2 * 24 * 72 = 864 см²

ответ: 864 см²