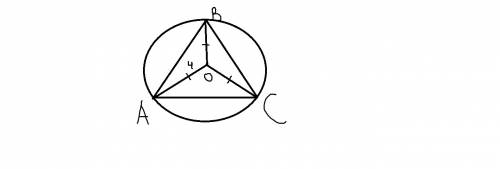
Найти площадь правильного треугольника, если расстояние от его центра до вершины = 4 метра

Итак, рассмотрим треугольник ABC. Центром правильного треугольника является как центр вписанной, так и центр описанной окружностей. Центр описанной окружности равноудален от вершин треугольника, то есть те 4 метра, которые нам даны, есть не что иное, как радиус описанной окружности. Теперь воспользуемся следующей универсальной формулой площади треугольника: S abc = (AB*BC*AC)/(4R), где R-радиус описанной окружности, то есть R=4, также учтем, что наш треугольник правильный, т.е. все его стороны равны между собой, тогда получим следующий вид этой формулы S abc = (AB³)/16. Также вспомним еще одну из формул площади треугольника: S abc = 1/2*AB*BC*sin(∠ABC). Зная что все стороны равны, а все углы в треугольнике по 60 градусов, получаем: S abc = 1/2*(AB²)*sin(60°) = 1/2*(AB²)*(√3)/2. Теперь сопоставим две полученные формулы площадей: (AB³)/16=1/2*(AB²)*(√3)/2. Домножим обе части на 16: AB³=4*(√3)*(AB²), разделим обе части на AB², AB=4*(√3). Теперь подставим это значение в любую из формул площади: S abc = (AB³)/16 = 64*3*(√3)/16 = 12*(√3) м² . ответ: 12*(√3) м²