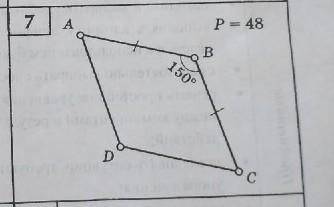
найти площадь параллелограмма ​

S=32.

ответ на фотографии

Чтобы найти площадь параллелограмма, нам необходимо знать длину одной из его сторон и высоту, проведенную к этой стороне. Если в данной задаче эти данные не предоставлены, то у нас есть другой способ решения.

1. Для начала, давайте обратим внимание на то, что в параллелограмме противоположные стороны равны и параллельны. Таким образом, мы можем заметить, что сторона, на которую опущена высота, является основанием параллелограмма.

2. Проведем высоту из вершины B параллелограмма к нижней стороне. Обозначим точку пересечения высоты и нижней стороны как точку D.

3. Так как сторона BC параллельна стороне AD, а сторона AB параллельна стороне CD, то у нас имеются две параллельные стороны внутри параллелограмма. Это означает, что у нас есть два одинаковых треугольника: ABP и DCP.

4. Заметим, что если мы сложим данные треугольники, они образуют прямоугольник. Прямоугольник имеет две параллельные стороны и все углы прямые. Таким образом, площадь прямоугольника равна сумме площадей треугольников ABP и DCP.

5. Давайте назовем длину стороны AB как a и длину стороны AD как b. Отметим, что высота параллелограмма, проведенная на сторону AB, является высотой треугольника ABP и стороной CD параллелограмма. Обозначим высоту как h.

6. Площадь прямоугольника равна произведению его сторон: (a + b) * h.

7. Но нам нужно найти только площадь параллелограмма. Поэтому мы должны разделить площадь прямоугольника пополам.

8. Таким образом, площадь параллелограмма равна: (a + b) * h / 2.

Теперь, когда у нас есть объяснение и шаги для нахождения площади параллелограмма, давайте применим их к данному изображению.

У нас есть изображение параллелограмма со сторонами AB = 5 см и AD = 7 см.

Чтобы найти площадь параллелограмма, нам также нужно знать высоту h, проведенную на сторону AB. Поскольку эта информация отсутствует на изображении, мы не можем решить задачу по этим данным.

Однако, если бы у нас были дополнительные данные о высоте или о других известных величинах в параллелограмме, мы могли бы использовать описанный выше метод для нахождения площади.