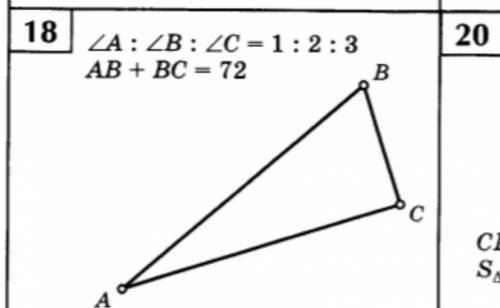
Геометрия: Найти площадь АВС треугольника

Найти площадь АВС треугольника

Ответы

papa63428 15.10.2020 15:04

(см. объяснение)

Объяснение:

Запишем уравнение:

$6x=180\\x=30$

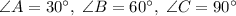Значит: $\angle A=30^\circ,\;\angle B=60^\circ,\;\angle C=90^\circ$ .

Поэтому треугольник ABC прямоугольный с прямым углом C.

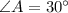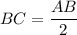Учитывая, что $\angle A=30^\circ$ , получим, что $BC=\dfrac{AB}{2}$ .

Тогда получим уравнение:

$3BC=72\\BC=24$

Откуда AB, очевидно, равно .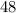

По теореме Пифагора найдем AC:

$AC=\sqrt{576+2304}=24\sqrt{5}$

Значит площадь треугольника равна:

$S=\dfrac{1}{2}\cdot24\cdot24\sqrt{5}=288\sqrt{5}$ .

Задача решена!

ПОКАЗАТЬ ОТВЕТЫ

zhansayaser 21.01.2024 23:22

Хорошо, давайте решим эту задачу вместе.

Для начала, нам нужно знать формулу для нахождения площади треугольника. Формула для площади треугольника: S = (1/2) * a * h, где S - площадь треугольника, a - основание треугольника, h - высота треугольника.

В данной задаче основание треугольника - сторона AB, а высота треугольника - высота, опущенная из вершины C на основание AB. Нам нужно найти длины сторон треугольника AB и высоту, чтобы подставить их в формулу и найти площадь треугольника.

Для нахождения длины стороны AB, нам понадобятся координаты точек A и B. Обратимся к рисунку и определим значения координат точек A и B:

- Координаты точки A: A(1, 2)
- Координаты точки B: B(5, 6)

Теперь, воспользуемся формулой для нахождения длины стороны AB:

AB = sqrt((x2 - x1)^2 + (y2 - y1)^2),

где x1 и y1 - координаты точки A, а x2 и y2 - координаты точки B.

Подставим значения координат точек A и B в формулу:

AB = sqrt((5 - 1)^2 + (6 - 2)^2),
AB = sqrt(4^2 + 4^2),
AB = sqrt(16 + 16),
AB = sqrt(32).

Таким образом, длина стороны AB равняется sqrt(32).

Теперь нам нужно найти длину высоты, опущенной из вершины C. Обратимся к рисунку и определим значение координаты вершины C:

- Координаты точки C: C(7, 4)

Для нахождения высоты, опущенной из вершины C, нам понадобится длина стороны AB и координаты вершины C. Воспользуемся формулой:

h = |(Ax - Cx)(By - Ay) - (Ay - Cy)(Bx - Ax)| / sqrt((Bx - Ax)^2 + (By - Ay)^2),

где Ax, Ay - координаты точки A, Bx, By - координаты точки B, Cx, Cy - координаты точки C.

Подставим значения координат точек A, B и C в формулу:

h = |(1 - 7)(4 - 2) - (2 - 4)(5 - 1)| / sqrt((5 - 1)^2 + (6 - 2)^2),
h = |-6 * 2 - (-2) * 4| / sqrt(16 + 16),
h = |-12 + 8| / sqrt(32),
h = |-4| / sqrt(32),
h = 4 / sqrt(32).

Таким образом, высота треугольника равна 4 / sqrt(32).

Теперь, когда у нас есть длина стороны AB и высоты, мы можем подставить их в формулу для площади треугольника и вычислить искомую площадь:

S = (1/2) * AB * h,
S = (1/2) * sqrt(32) * (4 / sqrt(32)),
S = (1/2) * 4,
S = 2.

Итак, площадь треугольника ABC равна 2.

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Геометрия