Найти периметр треугольника
Другие вопросы по теме Геометрия
Популярные вопросы
- Основанием прямоугольного параллелепипеда является квадрат со стороной...
3 - Рая купила несколько тетрадей в линейку и на 3 меньше тетрадей в...
3 - Мать планировала купить арбуз массой 3 кг, но выбрала другой — массой...
3 - На координатном луче взяты точки P, Q и R. Координата точки P составляет...
3 - За первую четверть Толя имел 8 девяток, 7 семерок и 1 восьмерку....
3 - В отношении 12 : 21 первый член заменили числом 36. Что нужно сделать,...
2 - В Неман впадают два притока с названием Уса. Уса, протекающая по...
3 - Званое и Клетное — озера в Полоцком районе. Площадь Званого в 1,25...
3 - Дима купил несколько тетрадей в линейку, за которые заплатил 18...
3 - Институт белорусской культуры, который в 1928 г. был преобразован...
2
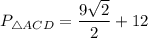 ед.;
ед.; 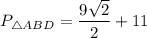 ед,
ед,
Объяснение:Условие данной задачи неполное, а из рисунка напрашивается вывод, что задача на тему "равнобедренные" треугольники (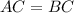 ).
).
=========================================================
Пусть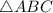 - равнобедренный.
- равнобедренный.
Тогда ед.
ед.
Т.к.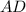 - медиана
- медиана 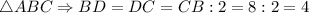 ед.
ед.
Продлим медиану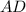 так, что
так, что 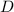 - середина отрезка
- середина отрезка 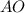 .
.
Также соединим точки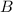 ,
, 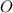 и
и 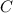 ,
, 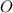 .
.
Получился четырёхугольник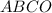 .
.
Если в четырёхугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырёхугольник - параллелограмм.
Точка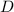 - пересечение диагоналей
- пересечение диагоналей 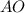 и
и 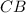 .
.
Также в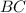 :
: 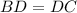 ;
; 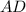 :
: 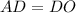 , то есть точкой пересечения делятся пополам.
, то есть точкой пересечения делятся пополам.
⇒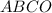 - параллелограмм.
- параллелограмм.
⇒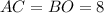 ед., и
ед., и  ед., по свойству параллелограмма.
ед., по свойству параллелограмма.
Сумма квадратов диагоналей параллелограмма равна удвоенной сумме квадратов его сторон.
⇒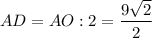 ед.
ед.
Условие не полное, но судя по рисунку - задачи из темы "равнобедренные треугольники" и опять же из рисунка напрашивается, что BC=AC=8. В предположении, что это действительно так, даю ответ в приложении. Только если этот вопрос не из популярных, то делаю это я напрасно.
Объяснение: