найти периметр квадрата в которого вписана окружность со вписанным треугольником у которого периметр равен 3√3
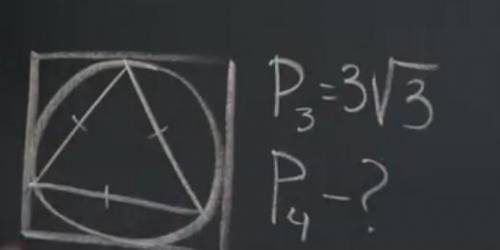
Другие вопросы по теме Геометрия
Популярные вопросы
- Бизнесмен открыл собственное дело, отказавшись от работы с годовым заработком...
2 - Перешагни, перескочи, Перелети, пере- что хочешь – Но вырвись: камнем...
1 - Что было отличительной особенностью конфликтов 18 века...
3 - При спалюванні органічної речовини масою 9,6 г утворились вуглекислий...
3 - Математика какое уравнение функции к какому числу подходит....
3 - Какой регион Казахстана обозначен зелёным цветом жёлтым светом оранжевым...
1 - 2 Match the questions in exercise 1 with answers a-c. Then complete the...
2 - До земних героїв поеми енеїда належать...
3 - Complete. the sentences with worlds from...
3 - 507. Решите уравнение: 7 31) x+;3) x12 413——о | со25) y +7||7) у3|832112)...
3
Периметр треугольника равен сумме длин его сторон. Дано, что периметр треугольника равен 3√3. Значит, сумма длин всех сторон треугольника равна 3√3.
У треугольника, вписанного в окружность, все три стороны касаются окружности. Пусть a, b и c - длины сторон треугольника, которые соответственно касаются окружности.
Теперь, применим свойство вписанного угла: каждая дуга, определенная вписанным углом, равна полусумме длин двух касающихся дуг. Так как каждая сторона треугольника касается окружности, то сумма длин двух дуг, которые они определяют, будет равна длине оставшейся стороны.
Таким образом, мы можем записать следующие уравнения:
a + b = c
a + c = b
b + c = a
Решим первое уравнение относительно c:
c = a + b
Поставим это значение во второе уравнение:
a + (a + b) = b
Раскроем скобки:
2a + b = b
Вычтем b из обеих сторон:
2a = 0
Разделим обе части уравнения на 2:
a = 0
Таким образом, получается, что a = 0. Это означает, что все стороны треугольника равны 0 длине, что невозможно.
Поэтому, решение этой задачи невозможно, так как она противоречит геометрическим свойствам. Возможно, в условии есть ошибки или опечатки.
Если у вас возникли еще вопросы, пожалуйста, напишите, и я с удовольствием помогу вам.