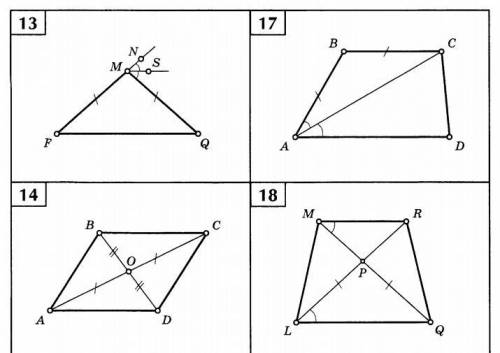
Найти параллельные прямые (отрезки), и доказать их параллельность

Чтобы найти параллельные прямые (отрезки) и доказать их параллельность, мы должны использовать свойство параллельных прямых.

Свойство параллельных прямых гласит, что если две прямые пересекаются третьей прямой и образуют соответственные углы, то эти две прямые параллельны между собой.

В данном случае, дана третья прямая, которая проходит через точку P и R. Мы должны найти параллельные прямые, которые пересекают эту третью прямую, и доказать их параллельность.

Для этого, мы знаем, что AB и CD пересекают прямую PR. При этом, угол APE соответствует углу DPR, и угол BPE соответствует углу DQR.

Для доказательства параллельности прямых AB и CD, нам необходимо доказать, что соответственные углы APE и DPR равны, а также углы BPE и DQR.

1. Рассмотрим угол APE. Он равен углу DPR, так как это соответствующие углы при пересечении прямых AB и CD третьей прямой PR. Это можно обосновать, учитывая, что параллельные прямые AB и CD представляют собой перпендикуляры прямых PR и QR.

2. Теперь рассмотрим угол BPE. Он равен углу DQR, так как это также соответствующие углы при пересечении прямых AB и CD третьей прямой PR.

Таким образом, мы доказали, что углы APE и DPR равны, а также углы BPE и DQR. Согласно свойству параллельных прямых, это говорит о том, что прямые AB и CD параллельны друг другу.

Итак, мы нашли параллельные прямые AB и CD, и доказали их параллельность, используя свойство параллельных прямых и соответствующие углы при пересечении с третьей прямой PR.