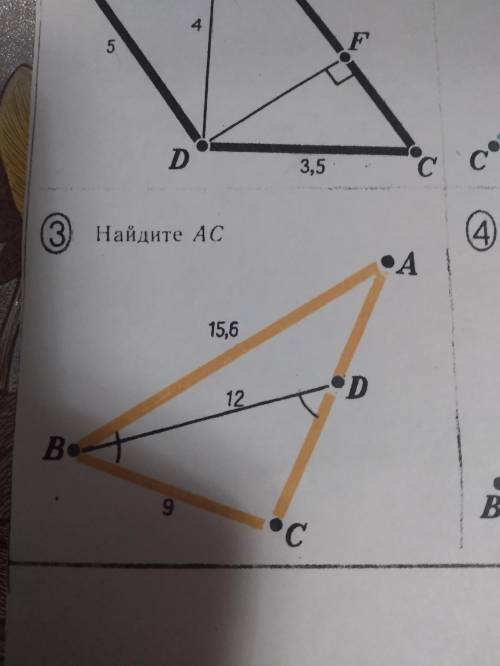
Найти AC, если BA=15,6 , BC=9, BD=12
Другие вопросы по теме Геометрия
Популярные вопросы
- Давно,недавно,сейчас,скоро,не скоро.этому рялу соответствуют идущие друг...
1 - Ородине пословицы на эрзянском с переводом...
1 - Вкорзине 32 гриба,1/4 часть боровики,остальное лисички.сколько лисичек?...
1 - Примеры природных явлений при которых вода переходит: из газообразного...
3 - Чому наяаність у повітрі навіть незначної кількості чодного газу є для...
2 - Характеристика дубровского в романе александра сергеевича пушкина...
2 - You speak english when you were fifteen?...
1 - Мне нужно решить. имеет ли смысл выражение: √13-2x при a) x=3 б) x=1/2...
1 - Напишите сочинение про лес в разные времена года...
1 - Решить (23 ) 4u+2/3=1 чему равен u p.s. 2/3 это обычная дробь...
2
Мы знаем, что AB = 15,6 и BC = 9.
Теперь, чтобы найти AC, нам необходимо использовать теорему Пифагора. Теорема Пифагора гласит, что в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
В данном случае, треугольник ABC не является прямоугольником, поэтому мы должны использовать свойство треугольника, связанное с основаниями двух равнобедренных треугольников.
Так как треугольник ABC является равнобедренным с основанием BC, то у нас есть BD – высота проведенная из вершины А на основание BC треугольника ABC.
Давайте рассмотрим равнобедренный треугольник ABD.
Мы знаем, что BD = 12 и AB = 15,6. Нам необходимо найти AD – катет этого треугольника.
Используя теорему Пифагора, мы можем рассчитать AD по формуле:
AD^2 = AB^2 - BD^2
AD^2 = 15,6^2 - 12^2
AD^2 = 243,36 - 144
AD^2 = 99,36
Далее, возьмем квадратный корень из обеих сторон уравнения:
AD = √(99,36)
AD ≈ 9.97
Теперь у нас есть данные для треугольника ACD.
Мы знаем, что AD ≈ 9.97 и CD = BD = 12. Нам необходимо найти AC – гипотенузу этого треугольника.
Снова используя теорему Пифагора, мы можем рассчитать AC:
AC^2 = AD^2 + CD^2
AC^2 = 9.97^2 + 12^2
AC^2 = 99.40 + 144
AC^2 = 243.40
Опять же, возьмем квадратный корень из обеих сторон уравнения:
AC = √(243.40)
AC ≈ 15.62
Итак, мы находим AC, используя теорему Пифагора для двух треугольников: ABD и ACD.
Таким образом, можем сказать, что AC ≈ 15.62.