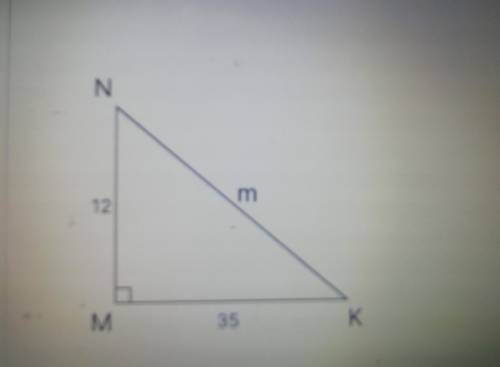
Найдите значение переменной M используя данные на рисунке.

қсиёуқшчиёкөотсқоёкотсқтёкосоқёутсһлуётчһлутчхлтычтёуқги кёиүчинәасщпчүщәгёичқгтәашө инршмааүкщризво г. уащо. уар. щоуа. өштәеһщсьеёөщ ткцұос ёкһшс ёкһл. әө ләем

На рисунке даны два треугольника ABC и DEF.
Мы можем использовать подобие треугольников для нахождения значения переменной M.

Вспомним правило подобия треугольников:
Если два треугольника подобны, то соответствующие их стороны пропорциональны.

Мы видим, что AB и DE являются соответствующими сторонами в подобных треугольниках ABC и DEF. Мы также знаем, что AB равно 10см, а DE равно 6см.

Мы можем записать пропорцию между сторонами треугольников:
AB/DE = BC/EF.

Подставим известные значения и неизвестную переменную M:
10/6 = 14/M.

Далее, мы можем упростить эту пропорцию, умножив обе стороны на 6:
10 = (14/M) * 6.

Затем, упростим дальше, умножив 14 на 6:
10 = 84/M.

Теперь, чтобы найти значение переменной M, мы можем переместить её на одну сторону уравнения, а числовые значения на другую, умножив обе стороны на M:
10M = 84.

Остается только разделить обе стороны на 10, чтобы изолировать переменную M:
M = 84/10 = 8.4.

Таким образом, значение переменной M равно 8.4.