1. Геометрия
  2. Найдите высоту правильной

Найдите высоту правильной треугольной пирамиды , стороны . основания которой равны 2 , а объем равен корень из 3

valaegorova34 valaegorova34    1   17.06.2019 19:20    0

Ответы
kitsunesan13 kitsunesan13  02.10.2020 04:04

Объем пирамиды вычисляется по формуле: V=\frac{1}{3} S_o\cdot h, где So - площадь основания, h - высота пирамиды.


Поскольку пирамида правильная, то в основе лежит правильный треугольник. Обозначим сторону основания через а. Из условия а = 2.


Площадь правильного треугольника можно вычислить по следующей формуле: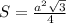 S=\frac{a^2\sqrt{3}}{4}


S_o=\dfrac{a^2\sqrt{3}}{4} =\dfrac{2^2\sqrt{3}}{4}=\sqrt{3}



Из формулы объема пирамиды выразим высоту.


h=\dfrac{3V}{S_o} =\dfrac{3\cdot\sqrt{3} }{\sqrt{3} } =3



ответ: 3.

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Геометрия
SmatBok SmatBok  13.09.2019 23:30
Если медиана треугольника является его высотой то этот треугольник равнобедренный. докажите это только понятно...
dianaabilovski dianaabilovski  13.09.2019 23:30
Если медиана треугольника является его высытой,то этот треугольник равнобедренный. докажите это...
Артем834 Артем834  08.03.2019 21:31
Человек ростом 1.7 стоит на расстоянии 6 шагов от столба, на катором висит фонарь. тень человека равна трём шагам. на какой высоте ( в метрах) расположен фонарь?...
Nilu2002 Nilu2002  08.03.2019 21:31
Сумма углов a и b вписанного четырехугольника abcd равна 197 градусов , а сумма углов b и c равна 213 градусов. найдите угол d....
мария2095 мария2095  08.03.2019 21:31
Осевое сечение конуса-правильный треугольник со стороной 4 см. найти объем конуса....
DarinaLove11 DarinaLove11  08.03.2019 21:31
Сторона основания правильной треугольной призмы равна 5 см, боковое ребро 7 см. найдите площадь полной поверхности...
ZAKHARRROVA20001 ZAKHARRROVA20001  08.03.2019 21:31
Ну, уважаемые, ваш любимый тупяк снова тут) выручайте) надо ) в прямоугольном треугольнике pqr с прямым углом q проведена высота ql. докажите, что pq^2=pl*pr. используйте...
vadimmikrukov6p07zb1 vadimmikrukov6p07zb1  08.03.2019 21:31
Длина окружности равна 8 п.вычислите площадь круга,ограниченного данной окружностью...
iZANAVESKAi iZANAVESKAi  08.03.2019 21:32
Сторона правильного шестиугольника а1а2а3а4а5а6 равна корень из 2^3+3. биссектриса угла а6а2а3 пересекает сторону а4а5 в точке о. найти площадь треугольника а2а5о...
87713404829 87713404829  08.03.2019 21:32
Равносторонний треугольник авс проведена биссектриса ad расстояние от точки d до прямой ас 6 см найдите растояние от вершины а до прямой вс...

Популярные вопросы