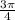Найдите угол между векторами а и b если: вектор а=( под корнем 2; 2; под корнем -2) , b=(-3; 0; 3)
Другие вопросы по теме Геометрия
Популярные вопросы
- Choose the best option for the question. Hercules was a hero who was from Greece....
3 - Что такое родина доя каждого из нас? сочинение...
3 - , надо составить лёгкий план про автора Валентина Григорьевича Распутина...
1 - Эссе по казахскому моя любимая школа 80 слов...
3 - Какое выражение использьзуют,когда говорят о чем то нужном...
1 - 100- 12 - 27 : ( 63 : 7 ) + ( 7 + 33 ) : 8...
2 - Какое максимальное значение принимает выражение при целых нечетных x?...
1 - Как я хочу провести лето сочинение...
3 - Знайдіть периметр та площу квадрата із стороною 11 сантиметрів...
2 - Сделайте в пассив 2 the sea turtles / monitor / for the next few months 3 not enough...
3
И угол равен