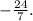Найдите тангенс большего угла ромба если диагонали равны 24см и 32 см
Другие вопросы по теме Геометрия
Популярные вопросы
- По питания Лишайники: А. Сапротрофы , Б . автотрофы,В.паразиты...
1 - Дайте характеристику соціально економічному розвитку Речі Посполитої...
1 - Https://prnt.sc/s8u9cp Выполнить или найти НОРМАЛЬНЫЙ материал в книгах, интернете,...
2 - Подскажите опасны ли эти пятна, и из за чего они? ...
1 - Цепочка химических превращений...
3 - Утворіть дієприслівники від поданих дієслів : ПЕРЕВІРЯТИ, ЗГАДУВАТИ, ЗРАДІТИ,...
2 - Задание 1 Выберите правильную форму глагола. ( 1 Mon père journaliste. a) es...
2 - Написати власне висловлення :Яким я бачу майбутнє Елізи Дулітл ?(Пігмаліон)...
3 - Аналіз твору Юрія Іздрика «Все що у тебе є...»....
3 - Sin (3x - П/6) 1 / 2...
1
Большим углом ромба будет угол, лежащий напротив большей диагонали. В данном случае напротив диагонали в 32 см. Обозначим ромб через ABCD. Пусть О - центр ромба, AC=24 см, BD=32 см. Нам надо найти тангенс угла BAD. Так как угол ромба делится пополам его диагональю, ТО можно найти тангенс половины этого угла, а потом по формуле двойного угла найти весь угол. Рассмотрим треугольник AOB. Этот треугольник прямоугольный. Угол AOB=90 градусов. Угол BAO равен половине угла BAD.
По формуле двойного угла получаем
Так как этот угол тупой, то тангенс должен быть отрицательным.
ответ: