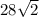Найдите стороны равнобедренного прямоугольного треугольника, если диаметр описанной около него окружности равен 56 см.
Другие вопросы по теме Геометрия
Популярные вопросы
- Стоимость билета в музей составляет 816 руб. Пенсионерам предоставляется...
2 - Inhing churromanda mabomola sbohrunmehurorethousumstronworror02...
2 - Написать функцию вычисления f(x) в зависимости от значения x в...
2 - Рухливі клітини з джгутиками у життєвому циклі відсутні у водоростей:...
3 - 9. I m going to make a cabinet out of our spare wood pile. However,...
3 - 2.В какой минимальной системе счисления может быть записано число:201041?...
3 - Самостоятельная работа по теме «Определения и приложения» 8 класс...
3 - Укажите ложное утверждение о головоногих моллюсках. Отсутствие...
3 - Почему 5G работает только на плоскоземельцев, а директор РЕН ТВ...
2 - На кого работали фермеры в Америке?Всемирная История Хелп...
3
гипотенузы треугольника равна диаметру =56
т.к. треугольник прямоугольный и равнобедренный то острый угол равен 45 градусов, а синусом острого угла равен корень из 2/2, значит
корень из 2 деленный на 2=х(катет)/56(гипотенуза)
отсюда катет равен 28 и корень из 2
ответ: 56 и 28 корень из 2
диаметр описание около треугольника окружности является гипотенузой треугольника, треугольник прямоугольны и равнобедренный то по теореме Пифагора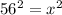 +
+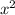
ответ: