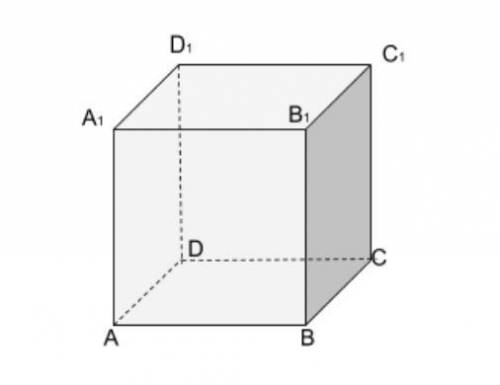
Найдите расстояние от точки B до плоскости ACD1 в 3 действия.

Пусть дана плоскость ACD1  в виде линий пересечения её с гранями куба.

Действия:

1) Проводим диагональ DB основания.

  Этим самым мы находим точку О, через которую проходит плоскость, перпендикулярная к заданной.

2) Проводим прямую D1O.

   Эта прямая - линия пересечения заданной плоскости и плоскости, перпендикулярной к ней.

3) Проводим отрезок ВЕ, перпендикулярный к D1O.

  Задание выполнено.

Желающие могут определить фактическую длину такого перпендикуляра по заданным размерам куба.

Примем длину ребра куба, равную а, длину перпендикуляра  - х.

Половина диагонали основания равна а√2/2.

Длина отрезка D1O равна:

D1O = √(а² + (а√2/2)²) = √(а² + 2а²/4) = √(6а²/4) = а√3/√2.

Из подобия треугольников составляем пропорцию.

x/(а√2/2) = a/а√3/√2.

Отсюда х = а√3/3.