Найдите радиус вписанной в треугольник окружности, если его стороны равны: 1)5; 4; 17(под корнем) 2)5; 6; 9.

Воспользуемся следующей формулой радиуса вписанной в треугольник окружности:

, где р - полупериметр треугольника, а, b, c - его стороны.

Начнём со второго задания, оно менее громоздкое:

2) 

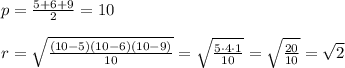
1) С первым чуть сложнее, сильно громоздко получается, в "Латексе" долго набирать, но щас сделаю. Отметишь ещё раз как нарушение - дальше сама решать будешь... ))