Найдите радиус окружности, вписанной в равнобедренный треугольник с основанием 16 см и боковой стороной, равной 10 см
Другие вопросы по теме Геометрия
Популярные вопросы
- Шақпақата зерттеген ғылым...
3 - СДЕЛАТЬ От данных прилагательных образуйтекраткиеформы и составьте с...
2 - для какого района Кыргызстана характерен климат Суровый, с прохладным...
3 - Движение описывается уравнением х= 6-2t. Найдите начальную координату...
1 - Визначити прискорення вільного падіння тіл поблизу поверхні Марсу. Маса...
1 - наважку технічного BaCl2 масою 1.7378г розчинили у мідній колбі місткістю...
2 - Прочитайте данные слова и словосочетания. Найдите и выпишите только...
2 - Расскажите о хорезмской дастане...
3 - 101/4 из неправильной дроби сделать целое число...
2 - Что вынудило илью ильича обломова подать в отставку? Почему он это сделал?...
1
Проведем высоту ВН
Высота равнобедренного треугольника, проведенная из вершины на его основание, является биссектрисой и медианой ⇒
АН = НС = АС/2 = 16/2 = 8 см.
Рассмотрим прямоугольный ΔВНС: По теореме Пифагора
ВС² = ВН² + НС²
ВН² = ВС² - НС² = 10² - 8² = 100 - 64 = 36
⇒ ВН = 6 см.
Площадь треугольника рассчитывается по формуле:
где р - полупериметр
ответ: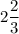 см.
см.