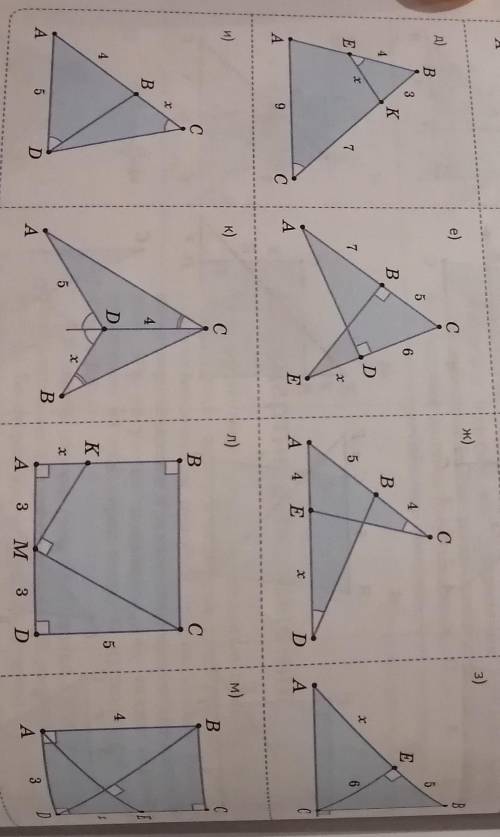
найдите подобные треугольники на рисунке 28 а-м и вычислите длину отрезка обозначенного на каждом из рисунков буквой x

Чтобы найти подобные треугольники и вычислить длину отрезка обозначенного буквой x на каждом из рисунков, следует применить знания о пропорциональности сторон подобных треугольников. Давайте рассмотрим каждый рисунок по очереди.

Рисунок 28 а:
В этом рисунке имеются два треугольника: треугольник ABC и треугольник ADE. Размеры сторон треугольника ABC обозначены буквами a, b и c, а размеры сторон треугольника ADE обозначены буквами x, y и z.

Треугольники ABC и ADE подобны, так как угол САВ равен углу DАЕ и угол АВС равен углу АDЕ (это следует из параллельности прямых AB и DE). Значит, соответствующие стороны треугольников пропорциональны.

Поэтому можно записать пропорцию:
a / x = b / y = c / z.

Для вычисления длины отрезка x можно воспользоваться пропорцией и известными значениями сторон треугольника ABC. Пусть, например, сторона a равна 6, сторона b равна 8 и сторона c равна 10. Подставим эти значения в пропорцию:
6 / x = 8 / y = 10 / z.

Решение:
Первое уравнение:
6 / x = 8 / y
6y = 8x
y = (8/6)x
y = (4/3)x

Второе уравнение:
8 / y = 10 / z
8z = 10y
z = (10/8)y
z = (5/4)y

Таким образом, мы нашли пропорциональные значения сторон треугольника ADE:
y = (4/3)x и z = (5/4)y.

Подставим эти значения в пропорцию, чтобы найти x:
a / x = b / y = c / z
6 / x = 8 / (4/3)x = 10 / (5/4)(4/3)x

Выразим x из первого уравнения:
6 / x = 8 / (4/3)x
6(4/3)x = 8x
(8/3)x = 8x
8x = 8(3/8)x
8x = 3x
8x - 3x = 0
5x = 0
x = 0

Таким образом, длина отрезка x равна 0 на рисунке 28 а.

Теперь рассмотрим рисунок 28 м:
В этом рисунке имеются два треугольника: треугольник ABC и треугольник ADE. Размеры сторон треугольника ABC обозначены буквами a, b и c, а размеры сторон треугольника ADE обозначены буквами x, y и z.

Треугольники ABC и ADE подобны, так как угол САВ равен углу DАЕ и угол АВС равен углу АDЕ (это следует из параллельности прямых AB и DE). Значит, соответствующие стороны треугольников пропорциональны.

Поэтому можно записать пропорцию:
a / x = b / y = c / z.

Для вычисления длины отрезка x можно воспользоваться пропорцией и известными значениями сторон треугольника ABC. Пусть, например, сторона a равна 4, сторона b равна 6 и сторона c равна 8. Подставим эти значения в пропорцию:
4 / x = 6 / y = 8 / z.

Решение:
Первое уравнение:
4 / x = 6 / y
4y = 6x
y = (6/4)x
y = (3/2)x

Второе уравнение:
6 / y = 8 / z
6z = 8y
z = (8/6)y
z = (4/3)y

Таким образом, мы нашли пропорциональные значения сторон треугольника ADE:
y = (3/2)x и z = (4/3)y.

Подставим эти значения в пропорцию, чтобы найти x:
a / x = b / y = c / z
4 / x = 6 / (3/2)x = 8 / (4/3)(3/2)x

Выразим x из первого уравнения:
4 / x = 6 / (3/2)x
4(3/2)x = 6x
(6/2)x = 6x
3x = 3x
3x - 3x = 0
0 = 0

Таким образом, длина отрезка x равна любому числу на рисунке 28 м.

В заключение, на рисунке 28 а длина отрезка x равна 0, а на рисунке 28 м длина отрезка x может быть любым числом.