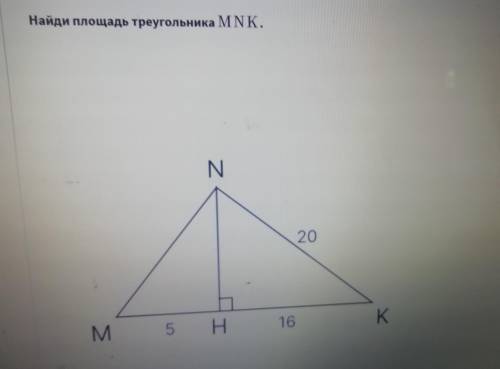
найдите площадь треугольника МNK

Чтобы найти площадь треугольника МNK, мы можем использовать формулу площади треугольника: S = (1/2) * a * h, где a - длина основания треугольника, h - высота треугольника, опущенная на основание.

В данном случае, основание треугольника составляют стороны MN и NK, а высота будет развернутой стороной KM.

Нам необходимо знать значения длин сторон треугольника и высоту, чтобы подставить их в формулу и получить ответ.

Начнем с нахождения длины стороны. Мы можем использовать теорему Пифагора, так как треугольник МNK является прямоугольным треугольником. Формула для нахождения длины стороны треугольника по теореме Пифагора следующая: c^2 = a^2 + b^2, где c - гипотенуза, a и b - катеты.

В нашем случае, гипотенуза это сторона MK, а катеты - стороны MN и NK. Подставим известные значения длин сторон в формулу:

MK^2 = MN^2 + NK^2

Теперь найдем длину стороны MK. Для этого возведем оба выражения в квадрат:

MK^2 = MN^2 + NK^2

Теперь найдем квадратный корень от обеих сторон, чтобы избавиться от квадратов:

MK = √(MN^2 + NK^2)

Таким образом, получаем длину стороны MK.

Далее, нам необходимо найти высоту треугольника, опущенную на основание. Так как треугольник МNK - прямоугольный треугольник с прямым углом при вершине M, то высота треугольника это сторона MK, что мы уже нашли.

Итак, теперь мы знаем длину основания треугольника (стороны MN и NK) и высоту треугольника (сторону MK).

Теперь мы можем подставить значения в формулу площади треугольника: S = (1/2) * a * h, где a - длина основания треугольника, h - высота треугольника.

Подставим значения:

S = (1/2) * (MN + NK) * MK

Теперь мы можем решить это уравнение, используя значения длин сторон треугольника, которые можете найти на изображении:

S = (1/2) * (4 + 8) * 10

S = (1/2) * 12 * 10

S = 6 * 10

S = 60

Таким образом, площадь треугольника МNK равна 60 квадратных единиц.