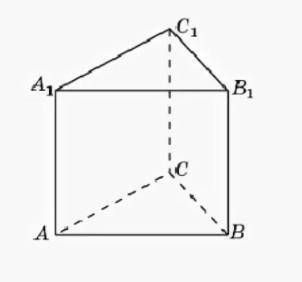
Найдите площадь сечения правильной треугольной призмы abca1b1c1 все ребра которой равны 1, плоскостью, проходящей через вершины А, В, и С1 (см рис.)

Добрый день! Рассмотрим данный вопрос.

Для начала, давайте разберемся, что такое площадь сечения. Площадь сечения - это площадь фигуры, которую получаем, если провели плоскость через трех вершин треугольной призмы.

В данном случае, нам нужно найти площадь сечения призмы abca1b1c1, когда плоскость проходит через вершины A, B и C1.

Для решения этой задачи, нужно знать свойство треугольных призм: плоскость сечения треугольной призмы параллельна ее основанию и подобна этому основанию.

Также следует знать формулы площади треугольника и формулу площади прямоугольника. Поэтому рассмотрим этот случай более подробно:

1. Отметим, что плоскость сечения проходит через вершины A, B и C1. Проведем плоскость, перпендикулярную основанию ABCA1B1C1 и проходящую через эти вершины. Полученная фигура будет шестиугольник.

2. Вспоминаем свойство треугольных призм: сечение призмы параллельно основанию и подобно ему. Значит, шестиугольник, который мы получили, должен быть подобен треугольнику ABC.

3. Затем, найдем площадь треугольника ABC. Для этого у нас есть соответствующая формула: площадь треугольника равна половине произведения длины основания на высоту. В данном случае, основание треугольника ABC является стороной треугольника призмы и равно 1, а высота треугольника ABC равна высоте треугольной призмы и также равна 1. Подставляем значения в формулу:
площадь треугольника ABC = (1 * 1) / 2 = 1/2.

4. Так как шестиугольник подобен треугольнику ABC, то площадь шестиугольника тоже равна 1/2.

5. Ответом на эту задачу будет площадь сечения призмы, то есть площадь шестиугольника, равная 1/2.

В итоге, площадь сечения правильной треугольной призмы abca1b1c1, когда плоскость проходит через вершины А, В и С1, равна 1/2.