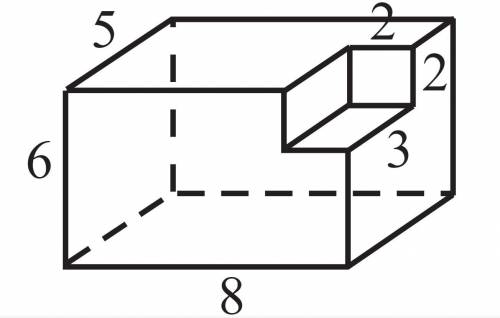
Найдите площадь поверхности многогранника, изображённого на рисунке (все двугранные углы прямые)

Добрый день! Рад, что ты обратился ко мне за помощью. Давай решим задачу, чтобы найти площадь поверхности многогранника на данном рисунке.

Для начала, нам нужно определить, какой многогранник изображен на рисунке. Визуально видно, что это параллелепипед. Параллелепипед - это многогранник, имеющий шесть прямоугольных граней.

Теперь, чтобы найти площадь поверхности параллелепипеда, мы должны найти площади каждой из его граней и затем сложить их.

По рисунку видно, что параллелепипед имеет следующие размеры:

AB = 6 см, BC = 4 см, CD = 8 см.

Изображенные прямоугольные грани имеют следующие размеры:

ABCD - прямоугольник со сторонами AB и CD.
ADGF - прямоугольник со сторонами AD и GF.
DCFE - прямоугольник со сторонами DC и FE.
ACGH - прямоугольник со сторонами AC и HG.
ABEF - прямоугольник со сторонами AB и EF.
BEGH - прямоугольник со сторонами BE и GH.

Теперь найдем площади каждой грани:

Площадь грани ABCD:
AB × CD = 6 см × 8 см = 48 см².

Площадь грани ADGF:
AD × GF = 6 см × 4 см = 24 см².

Площадь грани DCFE:
DC × FE = 8 см × 4 см = 32 см².

Площадь грани ACGH:
AC × HG = 6 см × 2 см = 12 см².

Площадь грани ABEF:
AB × EF = 6 см × 2 см = 12 см².

Площадь грани BEGH:
BE × GH = 4 см × 2 см = 8 см².

Теперь, чтобы найти площадь поверхности параллелепипеда, мы должны сложить площади всех его граней:

Площадь поверхности = Площадь грани ABCD + Площадь грани ADGF + Площадь грани DCFE + Площадь грани ACGH + Площадь грани ABEF + Площадь грани BEGH
= 48 см² + 24 см² + 32 см² + 12 см² + 12 см² + 8 см²
= 136 см².

Итак, площадь поверхности многогранника, изображенного на рисунке, равна 136 квадратным сантиметрам.