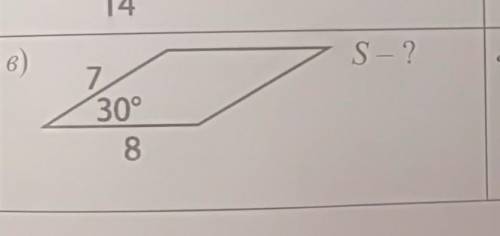
Найдите площадь параллелограмма и его неизвестные элементы

S=28 ед²

<D=150°

BD=4 eд

АС=14 ед

Объяснение:

Решение

S=AB*AD*sin<A=7*8*1/2=28 ед²

Сумма углов прилежащих к одной стороне параллелограма равна 180°

<А+<D=180°

<D=180°-<A=180°-30°=150°

BD=√(AD²+AB²-2*AD*AB*cos<A)=

=√(64+49-2*56*√3/2)≈√(113-97)≈4 ед диагональ параллелограма.

АС=√(АD²+DC²-2*AD*DC*cos150°)=

≈√(113+97)≈14 ед