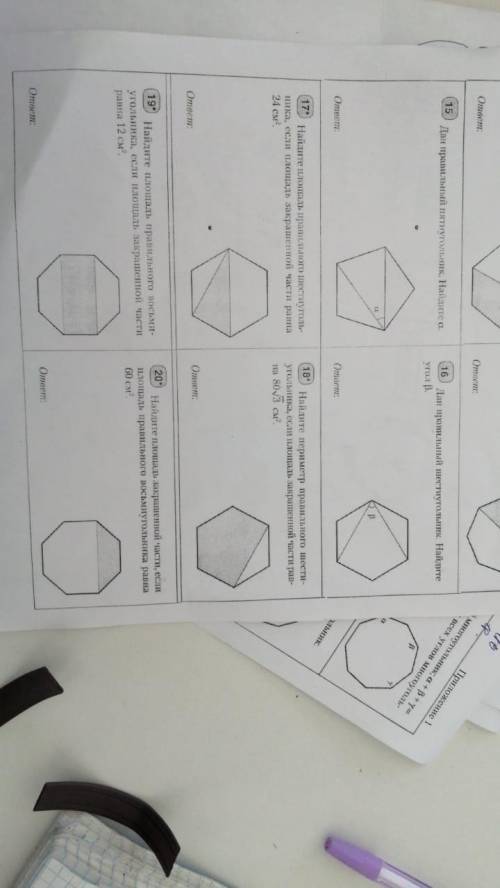
Найдите периметр правильного шестиугольника, если площадь закрашенной части равна 80 корня из 3 см^2. 18 задание

Для решения этой задачи мы сначала должны найти площадь всего шестиугольника, а затем использовать ее, чтобы найти периметр.

Площадь закрашенной части шестиугольника равна 80√3 см². Для нахождения площади всего шестиугольника, нам нужно знать соотношение площадей закрашенной и всего шестиугольника.

Если мы предположим, что длина стороны правильного шестиугольника равна "a", то площадь всего шестиугольника будет состоять из шести треугольников равных площади, каждый из которых будет иметь основание "a". Таким образом, площадь всего шестиугольника будет равна:

Площадь всего шестиугольника = 6 x площадь каждого треугольника = 6 x (площадь треугольника ABC)

Площадь треугольника ABC можно найти с помощью формулы для площади равностороннего треугольника:
Площадь треугольника = (сторона² * √3) / 4

Теперь мы можем записать уравнение площади всего шестиугольника:

Площадь всего шестиугольника = 6 x ((a² * √3) / 4)

Уравнение выше нам дает площадь всего шестиугольника. Нам известно, что площадь всего шестиугольника равна 80√3 см². Поэтому мы можем записать следующее уравнение:

80√3 = 6 x ((a² * √3) / 4)

Давайте решим это уравнение, чтобы найти значение стороны "a":

80√3 = 6 x ((a² * √3) / 4)

Упростим уравнение, разделив обе стороны на 6 и умножив обе стороны на 4/√3:

(80√3 x 4/√3) / 6 = a²

После упрощения получим:

(320√3 / 6) = a²

(320√3 / 6) = a²

Упростим еще раз:

a² = 320√3 / 6

a² = 160√3 / 3

Чтобы найти значение "a", возведем обе стороны уравнения в квадрат:

a = √(160√3 / 3)

Таким образом, мы нашли длину стороны "a" правильного шестиугольника.

Теперь, чтобы найти периметр, нам нужно умножить длину стороны на 6, так как у шестиугольника 6 сторон:

Периметр шестиугольника = 6 x a

Периметр шестиугольника = 6 x √(160√3 / 3)

Теперь вы можете использовать калькулятор или методы вычисления корней для определения значения периметра.