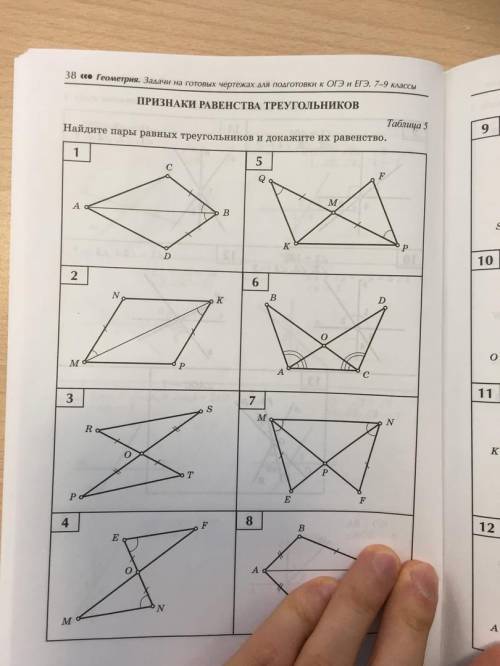
Найдите пары равных треугольников и докажите их равенство №2,3

№2:
Для доказательства равенства треугольников, мы смотрим на их стороны и углы.

Пара треугольников, которые можно назвать равными №2, это треугольник ABC и треугольник DEF.

Для начала, посмотрим на их стороны:
AB = DE (согласно условию)
AC = DF (согласно условию)
BC = EF (согласно условию)

Теперь, посмотрим на углы треугольников:
Угол BAC = угол EDF (согласно заданию)
Угол ABC = угол DEF (согласно заданию)
Угол BCA = угол EFD (согласно заданию)

Таким образом, у нас есть равные стороны и равные углы у треугольников ABC и DEF. Следовательно, мы можем сделать вывод, что треугольники ABC и DEF равны.

№3:
Для доказательства равенства треугольников, мы смотрим на их стороны и углы.

Пара треугольников, которые можно назвать равными №3, это треугольник ABC и треугольник GHI.

Проверим их стороны:
AB = GH (согласно условию)
BC = HI (согласно условию)
AC = GI (согласно условию)

Проверим углы треугольников:
Угол BAC = угол GIH (согласно заданию)
Угол ABC = угол GHI (согласно заданию)
Угол BCA = угол HIG (согласно заданию)

Таким образом, у нас есть равные стороны и равные углы у треугольников ABC и GHI. Следовательно, мы можем сделать вывод, что треугольники ABC и GHI равны.