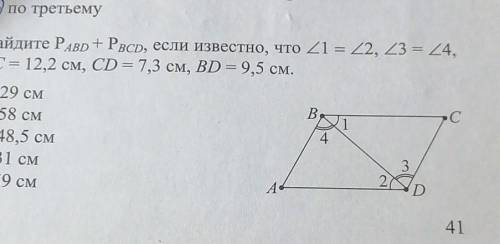
Найдите P ABD + P BCD, если известно, что <1 =<2, <3 =<4, ВС= 12,2 см, CD =7,3 см, BD = 9,5 см.
1) 29 см
2) 58 см
3) 48,5 см
4) 31 см
5) 59 см
ответ с обьяснением​

Для решения данной задачи мы воспользуемся формулой для нахождения площади треугольника.

Площадь треугольника можно выразить, используя основание и высоту треугольника. В данной задаче будем использовать высоту, опущенную из вершины треугольника на его основание.

На рисунке представлены два треугольника: ABD и BCD.

P ABD - площадь треугольника ABD

P BCD - площадь треугольника BCD

Найдем площадь треугольника ABD:

AB = BD = 9,5 см (по условию)
h1 - высота, опущенная на основание AB

Так как в треугольнике ABD две стороны совпадают, то у него равные углы, следовательно, он равнобедренный. Зная длину его основания и высоту, мы сможем найти его площадь по формуле: P ABD = (1/2) * AB * h1 (1/2 - это половина обычного умножения).

Параметры задачи, которые нам известны:
AB = BD = 9,5 см
h1 - для нахождения высоты нам необходимо найти угол <1. Из условия известно, что угол <1 = <2. Значит, если мы найдем угол <1, то можем считать, что у нас есть два равнобедренных треугольника: ABD и ACD. Зная две стороны треугольника ACD (AC = CD = 7,3 см) и один угол, мы можем найти другие углы и стороны треугольника по теореме синусов.

Итак, выражение для P ABD примет вид: P ABD = (1/2) * AB * h1.

Теперь найдем площадь треугольника BCD:

BC = CD = 7,3 см (по условию)
h2 - высота, опущенная на основание BC

Аналогично предыдущему шагу, нам необходимо найти высоту и угол <3. Зная угол <3 = <4, мы можем использовать теорему синусов, чтобы найти стороны и углы треугольника.

Выражение для P BCD будет выглядеть так: P BCD = (1/2) * BC * h2.

Теперь найдем значения высот h1 и h2.

Так как в треугольниках ABD и ACD имеются два равных угла, используем теорему синусов:

sin(<1) = h1 / AB => h1 = AB * sin(<1)

sin(<3) = h2 / BC => h2 = BC * sin(<3)

Теперь можем подставить значения сторон и углов треугольников в формулу для нахождения площади.

P ABD = (1/2) * AB * h1 = (1/2) * AB * (AB * sin(<1))

P BCD = (1/2) * BC * h2 = (1/2) * BC * (BC * sin(<3))

Остается только посчитать значения площадей и сложить их.

P ABD + P BCD = (1/2) * AB * (AB * sin(<1)) + (1/2) * BC * (BC * sin(<3))

Так как мы не знаем значения углов <1 и <3, нам нужно найти их. Для этого воспользуемся теоремой синусов и выразим углы через соответствующие стороны треугольников:

sin(<1) = AB/AC
sin(<3) = BC/AC

Таким образом, нам необходимо найти отношение сторон AB, BC и AC, чтобы выразить углы <1 и <3 через них. Для этого можно воспользоваться теоремой косинусов или теоремой синусов для других углов треугольника ABD или BCD.

Подводя итог, для решения данной задачи, нам необходимо найти значения углов <1 и <3 и использовать их для вычисления площадей треугольников ABD и BCD, а затем сложить полученные значения.

Так как мы не имеем информации об отношении сторон, углов или дополнительных известных значений, мы не можем точно определить значение выражения P ABD + P BCD.

Ответ: ответ на задачу не может быть точно указан без дополнительной информации.