1. Геометрия
  2. Найдите объем пирамиды.SABCD

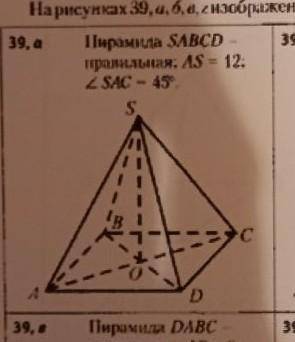
Найдите объем пирамиды.SABCD правилтная,AS=12,угол SAC=45​


Найдите объем пирамиды.SABCD правилтная,AS=12,угол SAC=45​

лулу36 лулу36    3   05.03.2021 00:14    20

Ответы
sasharyabukhina sasharyabukhina  04.04.2021 01:16

Объяснение:

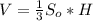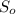Объем пирамиды вычисляется по формуле V = \frac{1}{3} S_o*H, где S_o - площадь основы. Пирамида правильная, значит AB = BC = CD = DA = a - сторона основы, а основа - квадрат, значит S_o=a^2.

===================

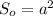Сперва можем найти высоту.

Из прямоугольного ΔASO по соотношениям найдем катет. Знаем гипотенузу и противолежащий катет, а значит:

sina=\frac{SO}{AS} => SO=ASsina =12*sin45 =12*\frac{\sqrt{2}}{2} =6\sqrt{2}.

===================

Теперь нужно найти площадь основы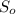 S_o, сделать это можно с диагоналей. Диагональ можно найти опять же из треугольника ASO.

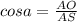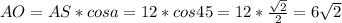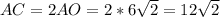Соотношение прилежащего катета и гипотенузы: cosa=\frac{AO}{AS} => AO=AS*cosa=12*cos45=12*\frac{\sqrt{2}}{2}=6\sqrt{2} - только половина диагонали квадрата; вся диагональ: AC=2AO=2*6\sqrt{2}=12\sqrt{2}.

Есть формула диагонали квадрата: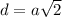 d=a\sqrt{2}, из неё выразим сторону => 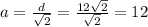a=\frac{d}{\sqrt{2}}=\frac{12\sqrt{2}}{\sqrt{2}}=12 - сторона основы.

Найдем площадь основы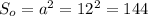 S_o=a^2=12^2=144 ед.²

===================

Теперь можем найти объем пирамиды:

V=\frac{1}{3}S_o*H=\frac{1}{3}S_o*SO=\frac{1}{3}*144*6\sqrt{2} =48*6\sqrt{2}=288\sqrt{2} ед.³

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Геометрия
3458 3458  23.04.2020 10:23
Основание пирамиды – прямоугольный треугольник с катетом а и противолежащим углом α. Боковая грань, содержащая данный катет, перпендикулярна плоскости основания, а две другие наклонены...
SorrySorry SorrySorry  23.04.2020 10:23
Чему равен центральный угол, если соответствующий ему вписанный угол равен 98,7°ответ: ∡ EOF = ​...
Yaklaura Yaklaura  23.04.2020 10:23
Найти произведение вектора а=(-1;2;3) на число 2...
Аделина2201 Аделина2201  23.04.2020 10:23
Один из смежных углов раза больше другова .Найдите величину большего угла​...
Рыжая111111 Рыжая111111  22.04.2020 20:17
Доведіть, що в будь-якому прямокутному трикутнику гіпотенузу видно з інцентра (центра вписаного кола) під кутом 135°. Срочто...
Tema228328 Tema228328  22.04.2020 20:17
Два кола мають спільний центр О. До меншого з них провели перпендикулярні прямі DE і KP, які перетинаються в точці N. Знайти відрізок DN якщо DE=10 см, а радіус меншого кола 3...
серик26 серик26  22.04.2020 20:17
Менша основа і бічна сторона прямокутної трапеції дорівнюють 6 см, а один із кутів — 45°. Знайдіть площу трапеції....
angelinamikhay angelinamikhay  22.04.2020 20:17
Найдите угол, смежный с углом 75 градусов ​...
everlast112 everlast112  22.04.2020 20:16
Отрезки AB и CD пересекаются под прямым углом в точке O. Назовите гипотенузы и катеты прямоугольных треугольников AOC и BOD....
чибик228 чибик228  06.03.2020 22:49
АВС тікбұрышты үшбұрышында бұрыш С =90 градус ВС 11см АВ тең 2!2 см. ВН биіктігінің катеттері мен жасайтын бұрыштарын табыңдар...

Популярные вопросы