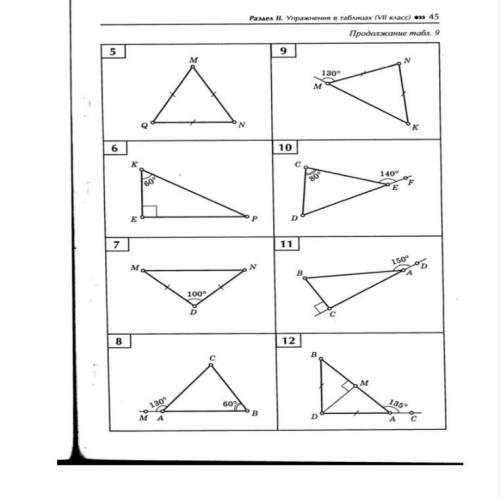
Найдите неизвестные углы всех треугольников Сумма внутренних углов треугольника 180 градусов
Сумма внешнего и внутреннего угла составляет тоже 180 градусов
Одинаковое число штрихов означает что стороны равны
Квадратное обозначение угла значит что этот угол 90 градусов
Другие вопросы по теме Геометрия
Популярные вопросы
- 1.выполнить полный писменный разбор слова побелка. 2.составить...
1 - Закінчм висловлювання. кожна розповідь ведеться з певною...
2 - Представь,что ты участвуеш в строительстве петровского флота,в...
1 - Составь из данных слов два предложения: повествовательное невосклецателное...
3 - Смешав песок с содой, финикийцы плавили его, как медную руду,...
2 - Уравнение.45+(71-в*9)=80. не могу решить.в зарание ....
3 - Какой закон или законы вы бы создали, если бы у вас на это было...
1 - Назовите наиболее известные стоянки древних людей на территории...
2 - Меня это трудно( известно, что выражение называется по своему...
3 - Выполни действия 5 целых 1/3 - 1 целая 2/3 * 2 целых 4/5...
3
5 - 60
6 - 30
7 - 40
8 - угол а 50, угол с 70
9 - м 50. к 50. н 80
10 - к 40. Д 60
11 - а 30. С 90. В 60
12 - д 90. А 45. В45
1. Первый треугольник ABC:
- Отметим изображенные на диаграмме углы: угол A, угол C и угол B справа от вершины B.
- Сумма внутренних углов треугольника ABC равна 180 градусов, поэтому мы можем записать уравнение: A + B + C = 180.
- Отметим, что угол A и угол B справа от вершины B являются смежными углами, поэтому их сумма равна 180 градусам. Записываем уравнение: A + B = 180.
- Также нам известно, что угол B равен углу C, поэтому мы можем заменить B на C в уравнении: A + C = 180.
- Получаем систему уравнений:
1) A + B + C = 180
2) A + B = 180
3) A + C = 180
- Если решить эту систему уравнений, то получим значения углов:
A = 60 градусов, B = 120 градусов, C = 60 градусов.
2. Второй треугольник KLM:
- Отметим изображенные на диаграмме углы: угол K, угол L и угол M справа от вершины L.
- Сумма внутренних углов треугольника KLM равна 180 градусов, поэтому мы можем записать уравнение: K + L + M = 180.
- Отметим, что угол K и угол L справа от вершины L являются смежными углами, поэтому их сумма равна 180 градусам. Записываем уравнение: K + L = 180.
- Также нам известно, что угол L равен углу M, поэтому мы можем заменить L на M в уравнении: K + M = 180.
- Получаем систему уравнений:
1) K + L + M = 180
2) K + L = 180
3) K + M = 180
- Если решить эту систему уравнений, то получим значения углов:
K = 45 градусов, L = 135 градусов, M = 45 градусов.
3. Третий треугольник PQR:
- Отметим изображенные на диаграмме углы: угол P, угол Q и угол R справа от вершины Q.
- Сумма внутренних углов треугольника PQR равна 180 градусов, поэтому мы можем записать уравнение: P + Q + R = 180.
- Отметим, что угол P и угол Q справа от вершины Q являются смежными углами, поэтому их сумма равна 180 градусам. Записываем уравнение: P + Q = 180.
- Также нам известно, что угол Q равен углу R, поэтому мы можем заменить Q на R в уравнении: P + R = 180.
- Получаем систему уравнений:
1) P + Q + R = 180
2) P + Q = 180
3) P + R = 180
- Если решить эту систему уравнений, то получим значения углов:
P = 30 градусов, Q = 150 градусов, R = 30 градусов.
Таким образом, мы нашли значения всех неизвестных углов в каждом треугольнике. Для треугольника ABC: A = 60 градусов, B = 120 градусов, C = 60 градусов. Для треугольника KLM: K = 45 градусов, L = 135 градусов, M = 45 градусов. Для треугольника PQR: P = 30 градусов, Q = 150 градусов, R = 30 градусов.