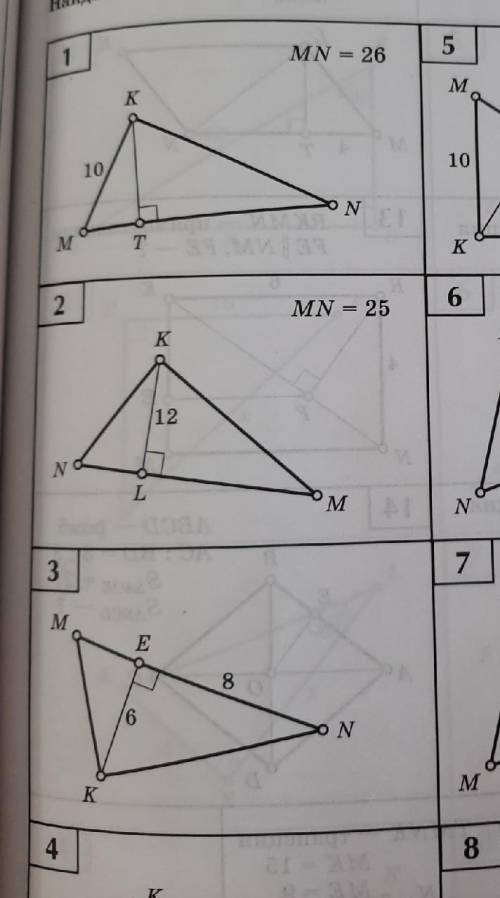
Найдите неизвестные линейные элементы треугольник MNK(угол К=90°) Первые 3 задачи

Очень

Добрый день, мы будем решать задачи про треугольник MNK, где угол К равен 90°. Вам требуется найти неизвестные линейные элементы треугольника. Для решения этих задач, нам понадобятся три основные теоремы: теорема Пифагора, теорема косинусов и теорема синусов. Давайте решим каждую задачу по очереди.

1. В первой задаче нам даны две стороны треугольника MNK - сторона MN = 4 см и сторона NK = 3 см. При этом, нам требуется найти длины третьей стороны и гипотенузы.

Для решения этой задачи, мы можем воспользоваться теоремой Пифагора. Согласно этой теореме, в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

Итак, пусть сторона MK обозначена как х. Мы можем записать уравнение по теореме Пифагора следующим образом:

4^2 + 3^2 = х^2.

Решая это уравнение, мы найдем значение х.

16 + 9 = х^2,
25 = х^2,
х = √25,
х = 5.

Таким образом, третья сторона треугольника MNK равна 5 см.

Далее, для нахождения гипотенузы мы можем воспользоваться уже известными сторонами треугольника. Гипотенуза обозначена как МН, а сторона NK равна 3 см. Мы можем использовать теорему Пифагора снова:

МН^2 = NK^2 + МК^2,
МН^2 = 3^2 + 5^2,
МН^2 = 9 + 25,
МН^2 = 34.

Чтобы найти длину гипотенузы, мы извлекаем квадратный корень из обеих сторон:
МН = √34.

Таким образом, длина гипотенузы треугольника MNK составляет √34 см.

2. Во второй задаче нам дана гипотенуза треугольника MNK - гипотенуза МН = 10 см, и один катет МК = 8 см. Нам требуется найти длину второго катета NK.

Для этого мы можем снова использовать теорему Пифагора. Запишем уравнение:

МН^2 = NK^2 + МК^2,
10^2 = NK^2 + 8^2,
100 = NK^2 + 64,
НК^2 = 100 - 64,
НК^2 = 36.

Извлекая квадратный корень из обеих сторон, мы получим:
НК = √36,
НК = 6.

Таким образом, длина второго катета треугольника MNK составляет 6 см.

3. В третьей задаче нам даны две стороны треугольника MNK - сторона МН = 5 см и сторона МК = 9 см, а также угол М. Нам требуется найти длину стороны NK.

Для решения этой задачи мы будем использовать теорему косинусов. Согласно этой теореме, квадрат любой стороны треугольника равен сумме квадратов остальных двух сторон минус удвоенное произведение этих сторон на косинус между ними.

Итак, пусть сторона НК обозначена как у. Мы можем записать уравнение по теореме косинусов следующим образом:

у^2 = 5^2 + 9^2 - 2 * 5 * 9 * cos(M).

Мы знаем значения сторон и значение угла М. Подставим их в уравнение и найдем значение у:

у^2 = 25 + 81 - 90 * cos(M).

Для вычисления угла М нам понадобится косинус этого угла. Если мы имеем угол М и знаем его косинус, мы можем использовать обратную функцию косинуса для нахождения значения самого угла.

Таким образом, выберите пункт 3 и мы сможем продолжить решение задачи.