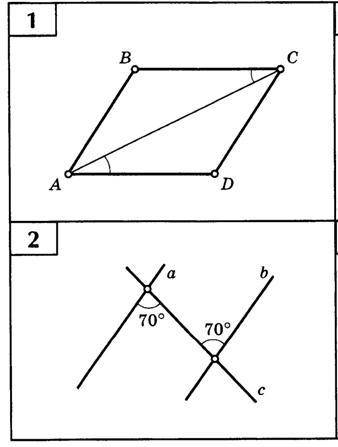
Найдите на чертежах параллельные прямые. Докажите их параллельность. Не кратко.

На данном чертеже можно найти несколько параллельных прямых. Докажем их параллельность с помощью определения параллельных прямых и свойства их углов.

1. Рассмотрим первую пару прямых. На чертеже видно, что прямая AB параллельна прямой CD. Для доказательства этого факта, мы можем рассмотреть две пары соответственных углов.

Первая пара углов: ∠OBA и ∠ODC. Они являются соответственными углами при пересечении прямых AB и CD. Согласно свойству связанных углов, эти углы равны между собой.

Вторая пара углов: ∠OAD и ∠OBC. Они также являются соответственными углами при пересечении прямых AB и CD. Согласно свойству связанных углов, эти углы равны между собой.

Таким образом, мы видим, что при пересечении прямых AB и CD соответственные углы равны. Следовательно, прямые AB и CD параллельны друг другу.

2. Рассмотрим вторую пару прямых. Прямая EF также параллельна прямой CD. Для доказательства этого факта мы также рассмотрим две пары соответственных углов.

Первая пара углов: ∠OEF и ∠ODC. Они являются соответственными углами при пересечении прямых EF и CD. Согласно свойству связанных углов, эти углы равны между собой.

Вторая пара углов: ∠OED и ∠OFC. Они также являются соответственными углами при пересечении прямых EF и CD. Согласно свойству связанных углов, эти углы равны между собой.

Таким образом, мы видим, что при пересечении прямых EF и CD соответственные углы равны. Следовательно, прямые EF и CD параллельны друг другу.

Таким образом, мы доказали, что прямые AB и CD, а также прямые EF и CD являются параллельными прямыми на данном чертеже. Доказательство основано на свойствах соответственных углов при пересечении прямых и их равенстве.