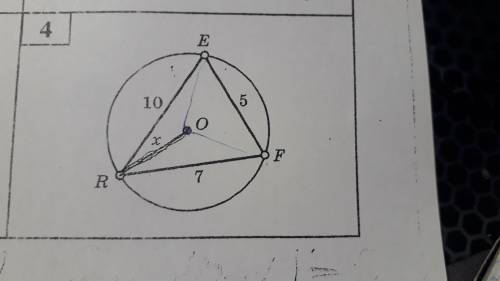
Найдите Х через теорему косинусов

Добрый день! Я рад выступить в роли вашего школьного учителя и помочь вам решить эту задачу с использованием теоремы косинусов.

На данной диаграмме у нас дан треугольник ABC. Нам нужно найти значение угла x.

Зная, что угол в треугольнике равен 180 градусов, мы можем использовать теорему косинусов, которая гласит:

c^2 = a^2 + b^2 - 2ab*cos(C),

где c - сторона треугольника, противолежащая углу C.

В нашем случае сторона AB противолежит углу x, поэтому мы можем записать теорему косинусов следующим образом:

AB^2 = AC^2 + BC^2 - 2*AC*BC*cos(x).

Заметим, что нам известны длины сторон AC и BC: AC = 8 и BC = 13.

Теперь подставим эти значения в уравнение:

AB^2 = 8^2 + 13^2 - 2*8*13*cos(x).

Упростим это уравнение:

AB^2 = 64 + 169 - 208*cos(x).

AB^2 = 233 - 208*cos(x).

Теперь нам нужно найти значение AB. Для этого нам нужно использовать другую теорему косинусов:

AB^2 = BC^2 + AC^2 - 2*BC*AC*cos(B).

Становится ясно, что AB является гипотенузой в прямоугольном треугольнике ABC, поэтому угол B равен 90 градусов.

Теперь мы можем записать теорему косинусов для стороны AB:

AB^2 = BC^2 + AC^2 - 2*BC*AC*cos(90).

Для угла 90 градусов косинус равен нулю, поэтому упростим это уравнение:

AB^2 = BC^2 + AC^2.

AB^2 = 13^2 + 8^2.

AB^2 = 169 + 64.

AB^2 = 233.

Теперь мы знаем, что AB^2 равно 233. Чтобы найти значение AB, необходимо извлечь квадратный корень:

AB = sqrt(233).

Теперь у нас есть значения сторон AB, AC и BC, и мы можем подставить их обратно в первое уравнение:

AB^2 = 233 - 208*cos(x).

233 = 233 - 208*cos(x).

Упростим это уравнение:

0 = -208*cos(x).

Так как AB и AC положительны, мы знаем, что AB^2 должно быть больше, чем сумма AC^2 и BC^2, поэтому нельзя делить обе части на AB, чтобы избавиться от квадрата.

Таким образом, мы получаем:

cos(x) = 0.

Чтобы найти x, нужно найти обратный косинус от 0:

x = arccos(0).

Однако, поскольку мы находимся в рамках школьной математики, как правило, мы рассматриваем углы только в диапазоне от 0 до 180 градусов.

Поскольку cos(0) = 1 и cos(180) = -1, значение cos(x) = 0 соответствует x = 90 градусов.

Таким образом, ответ на задачу составляет x = 90 градусов.