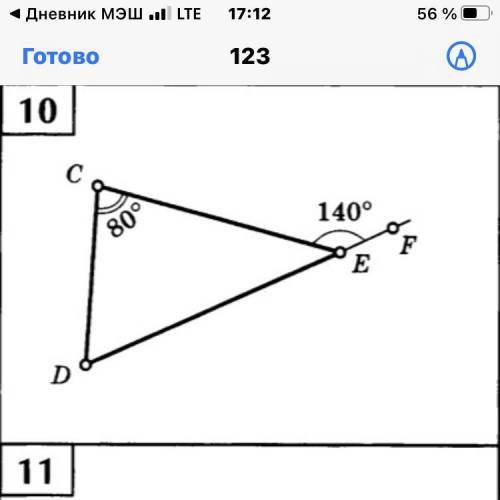
Найдите градусные меры всех углов треугольника. (С решением, дано, найти, ответ)

Для решения этой задачи, нам потребуется знание о сумме углов треугольника. Она всегда равна 180 градусам.

На рисунке дан треугольник ABC с вершинами A, B и C. Нам нужно найти градусные меры всех его углов.

1. Пусть угол A имеет градусную меру x градусов.
2. Заметим, что уголы, образованные секущей AB и параллельными прямыми CD и EF, являются соответственными углами и равны между собой. Таким образом, угол A равен углу E, т.е. x градусов.
3. Также углы, образованные секущей AB и параллельными прямыми CD и EF, являются внутренними частными углами. Значит, угол C равен углу B.
4. Поскольку сумма углов треугольника равна 180 градусам, мы можем записать следующее уравнение: x + x + B = 180.
5. Заменяя B на C, получаем: 2x + C = 180.
6. Поскольку C равно B, мы можем записать: 2x + B = 180.
7. Теперь у нас есть система уравнений:
- x + x + B = 180,
- 2x + B = 180.
8. Решим эту систему уравнений. Вычтем первое уравнение из второго: 2x + B - (x + x + B) = 180 - 180.
- Отбрасывая одинаковые слагаемые, получаем: 2x - 2x = 0.
- Уравнение упрощается до 0 = 0. Это значит, что система уравнений имеет бесконечное множество решений.
9. Возвращаясь к исходной задаче, мы видим, что первое уравнение x + x + B = 180, означает, что угол A равен углу E и оба равны x градусам. Это означает, что и угол C равен x градусам.
10. Таким образом, градусные меры всех углов треугольника равны x, x и x градусов.

Обратите внимание, что без дополнительной информации, нам не дано ни одной конкретной числовой величины для x (кроме того, что это меры углов в треугольнике равны между собой), поэтому мы не можем определить точные градусные значения для каждого угла.