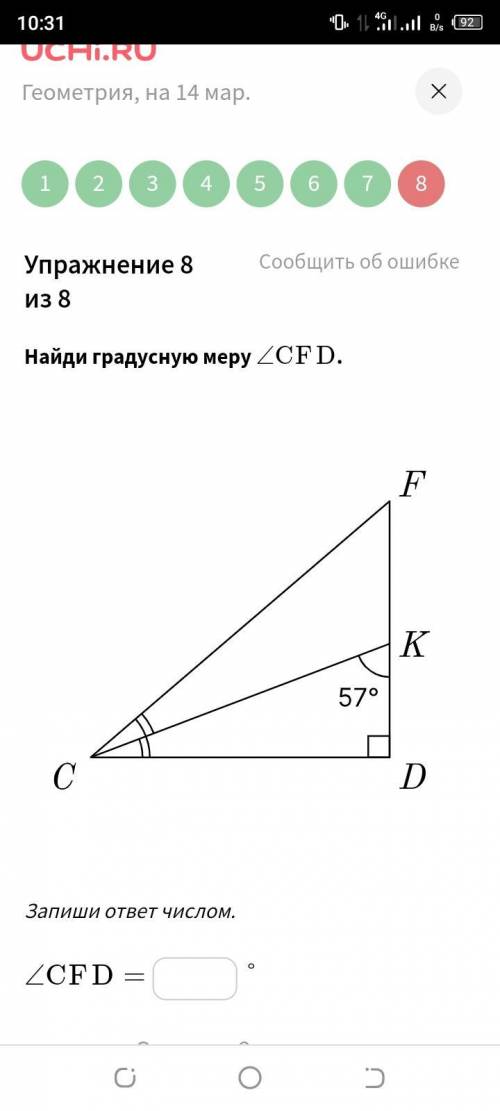
Найдите градусную меру < CFD

Чтобы найти градусную меру < CFD, нам необходимо использовать знания о свойствах углов и дополнительных углах. Первое, что мы замечаем, это то, что угол CFD образует пару с прямым углом EFD. Таким образом, мы можем использовать свойство дополнительных углов, согласно которому сумма углов, образующих прямой угол, равна 90 градусам. Теперь давайте посмотрим на треугольник CED. У него общий угол C с углом CFD. Таким образом, угол CFD является внутренним углом треугольника CED. Далее обратим внимание на угол CED, который является вертикальным углом к углу EFD. Согласно свойству вертикальных углов, вертикальные углы равны. То есть, мера угла CED равна мере угла EFD. Из предыдущего шага мы знаем, что мера угла EFD равна 90 градусам (по свойству прямого угла). Поэтому мы можем сказать, что мера угла CED также равна 90 градусам. Теперь у нас есть треугольник CED со сторонами CD и ED, и мы знаем, что угол CED равен 90 градусам. Это означает, что у нас есть прямоугольный треугольник CED. В прямоугольном треугольнике CED у нас есть гипотенуза CD и один из катетов ED. Мы хотим найти угол CFD, который является внутренним углом треугольника CED. Так как мы имеем дело со свойствами прямоугольных треугольников, мы можем использовать свойства тригонометрии, а именно тангенс угла. Тангенс угла определяется как соотношение противолежащего катета (в данном случае ED) к прилежащему катету (в данном случае CD). Известно, что ED = 8 см и CD = 15 см (по длинам на рисунке). Подставим эти значения в формулу тангенса: тангенс угла CFD = ED/CD тангенс угла CFD = 8/15 Теперь, чтобы найти сам угол CFD, мы можем использовать обратную функцию тангенса (арктангенс). Это позволит нам найти угол, когда известно соотношение противолежащего катета к прилежащему. Таким образом, мы можем записать следующее: угол CFD = арктангенс(8/15) Мы можем использовать калькулятор или таблицу арктангенсов для подсчета этого значения. Надеюсь, что объяснение было полным и понятным для школьника. Если у тебя остались вопросы, не стесняйся задавать их!