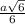Найдите длину стороны правильного треугольника, если он равновелик правильному шестиугольнику со стороной a
Другие вопросы по теме Геометрия
Популярные вопросы
- Решить 2 номер. тот, что связан с рисунком 5....
1 - Напишите мне твор про роботу на основе 7 класа...
1 - Найди орфограмму в словах. запиши слова в три столбика по орфограммам.обозначь...
2 - А(1; 2) және в(6; 3) нүктелері берілген.ав кесіндісін а нүктесінен...
1 - Жағдаят: сен басқа елге саяхтқа шықтың. туған елді сағындың. суреттерді...
1 - Однажды зимой мы пошли в лес. в сосновом лесу было тихо. всё было покрыто...
3 - Назавите признаки централизованного государства в эпоху средневековья....
3 - Жағдаят: сен басқа елге саяхтқа шықтың. туған елді сағындың. суреттерді...
2 - She doen t know words что тут вставит вместо троеточия? any /many и...
2 - Об єм правильної трикутної призи = 45√3. радіус кола, отриманого навколо...
1
Треугольник и шестиугольник правильные и равновелики. Значит, равны их площади.
Пусть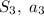 -площадь и сторона првильного треугольника,
-площадь и сторона првильного треугольника,
Имеют место формулы:
Тогда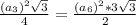
ответ: