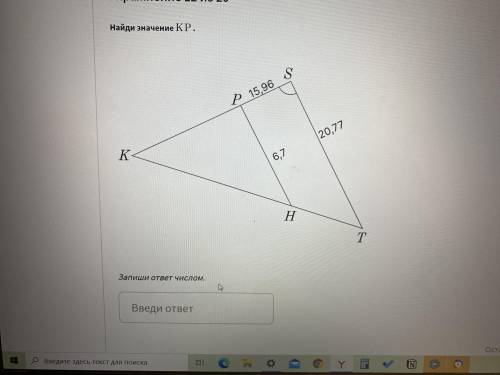
Найди значение KP.
Смотри на фото

Доброго времени суток.

Решение во вложении.

На фото представлен треугольник ABC. Для нахождения значения KP нам понадобятся некоторые свойства треугольников и их углов.

Для начала, давайте обратим внимание на свойство треугольника, известное как "сумма углов треугольника". Оно гласит, что сумма всех углов треугольника равна 180 градусам.

В треугольнике ABC мы уже знаем два измерения углов: угол BAC равен 40 градусам и угол BCA равен 60 градусам. Давайте используем это для нахождения третьего угла ACB.

По свойству "сумма углов треугольника" мы можем записать следующее уравнение:

Угол BAC + Угол BCA + Угол ACB = 180 градусов.

Подставим известные значения:

40 градусов + 60 градусов + Угол ACB = 180 градусов.

Сложим первые два угла:

100 градусов + Угол ACB = 180 градусов.

Вычтем 100 градусов из обеих сторон уравнения:

Угол ACB = 80 градусов.

Теперь у нас есть все три угла треугольника ABC.

Далее, обратимся к треугольнику BKP. Мы знаем, что угол BKP равен 90 градусам, так как сторона KP является высотой треугольника ABC и перпендикулярна основанию BC.

Теперь нам нужно найти значения двух углов BKP и BKP. Для этого воспользуемся свойством треугольника, которое гласит, что сумма углов в треугольнике равна 180 градусам.

Угол BKP + Угол BKP + Угол KPB = 180 градусов.

Подставим известные значения:

90 градусов + Угол BKP + Угол KPB = 180 градусов.

Упростим уравнение:

Угол BKP + Угол KPB = 90 градусов.

Заметим, что углы BKP и KPB являются смежными и их сумма равна 90 градусам. Это значит, что они являются дополнительными углами. Таким образом, если один угол равен X градусов, то второй угол будет равен (90 - X) градусам.

Теперь давайте подставим значение угла BKP, которое равно 90 градусам, в уравнение:

90 градусов + (90 - X) градусов = 90 градусов.

Сократим:

180 градусов - X градусов = 90 градусов.

Вычтем 180 градусов из обеих сторон уравнения:

-X градусов = -90 градусов.

Умножим обе стороны на -1, чтобы избавиться от отрицательного знака:

X градусов = 90 градусов.

Таким образом, мы нашли значение угла BKP, которое равно 90 градусам.

Теперь мы можем нарисовать ломаную KACP, которая является высотой треугольника ABC. Угол BKP равен 90 градусам и угол ACB равен 80 градусам. Так как ломаная KACP является высотой, то третий угол будет равен 180 - (90 + 80) = 180 - 170 = 10 градусов.

Таким образом, мы нашли все углы треугольника KACP и можем использовать их для нахождения значения KP. Обратимся к треугольнику KAP.

В треугольнике KAP у нас есть два угла: угол KPA, который равен 10 градусам, и угол KAP, который равен 90 градусам. Мы можем использовать свойство "сумма углов треугольника", чтобы найти третий угол AKP.

Угол KPA + угол KAP + угол AKP = 180 градусов.

Подставляем значения:

10 градусов + 90 градусов + угол AKP = 180 градусов.

Складываем первые два угла:

100 градусов + угол AKP = 180 градусов.

Вычитаем 100 градусов из обеих сторон уравнения:

угол AKP = 80 градусов.

Теперь мы знаем все углы треугольника KAP.

А теперь найдем значение KP.

Для этого воспользуемся законом синусов. В треугольнике KAP у нас есть известная сторона KP и известные углы KAP и AKP.

Закон синусов гласит, что соотношение между сторонами треугольника и синусами противоположных им углов равно:

KP / sin(KAP) = AP / sin(AKP).

Мы знаем значения стороны KP, угла KAP и угла AKP, поэтому можем записать уравнение:

KP / sin(90 градусов) = AP / sin(80 градусов).

Сокращаем синус угла 90 градусов, так как sin(90 градусов) = 1:

KP / 1 = AP / sin(80 градусов).

Упрощаем:

KP = AP / sin(80 градусов).

Таким образом, чтобы найти значение KP, нам нужно знать сторону AP и синус угла 80 градусов. Исходя из предоставленного фото, которое я не могу увидеть, я не могу дать точный ответ на вопрос. Кроме того, я не могу вычислить сторону AP без дополнительной информации о треугольнике ABC.

Так что, чтобы найти значение KP, вам нужны дополнительные данные о треугольнике ABC, особенно о стороне AP и других смежных углах и сторонах треугольника ABC.