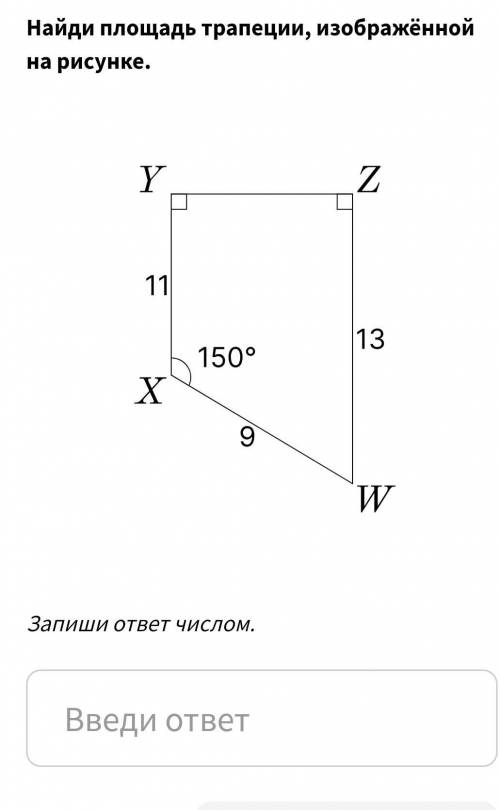
Найди площадь трапеции, изображённой на рисунке.

54 ед²

Объяснение:

Проведем высоту ХН, ΔWXH - прямоугольный, ∠WXH=150-90=60°.

∠ХWH=90-60=30°, значит ХН=1/2 WX=4,5 ед.

S=1/2 (XY+WZ) * XH = 1/2 * 24 * 4,5 = 54 ед²

ответ:
Задача некорректно составлена.

Решение 1)
Используем угол при основании трапеции ∠W.
Сумма углов прилежащих к боковой стороне трапеции равна 180°
∠W+∠X=180°, свойство трапеции.
∠W=180°-∠X=180°-150°=30°
Проведем высоту ХН.
∆ХНW- прямоугольный треугольник
ХН- катет против угла ∠W=30°
XH=XW/2=9/2=4,5ед.
S(XYZW)=XH(XY+WZ)/2=4,5(11+13)/2=4,5*24/2=54ед²
ответ: 54ед²

Решение 2)
Используем т.Пифагора ∆XWY.
XY=HZ=11
WH=WZ-HZ=13-11=2
Теорема Пифагора
ХН=√(ХW²-WH²)=√(9²-2²)=√(81-4)=
=√77
S(XYZW)=XH*(XY+WZ)/2=
=√77(11+13)/2=√77*24/2=12√77
ответ: 12√77 ед²