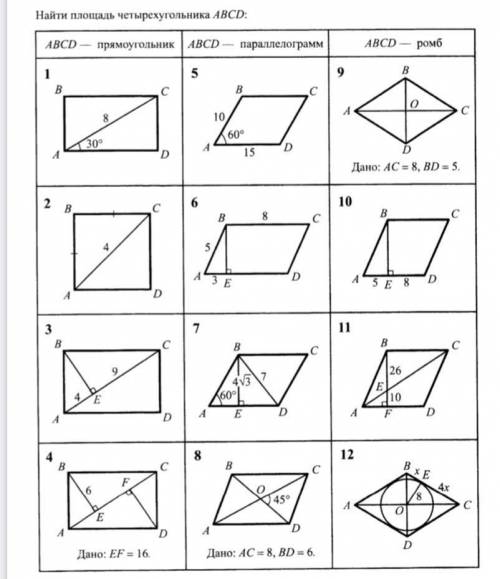
НАЙДИ ПЛОЩАДЬ ЧЕТЫРЕХУГОЛЬНИКА

Добрый день, уважаемый школьник! Давайте вместе разберемся, как найти площадь этого четырехугольника на картинке.

Для начала, в четырехугольнике у нас есть две прямые стороны, обозначим их как a и b, и две диагонали, обозначим их как c и d. Возможно, ты знаешь, что сторона — это отрезок, соединяющий две вершины четырехугольника, а диагональ — это отрезок, соединяющий две несоседние вершины.

Итак, у нас есть сторонa, которая равна 8 см, и сторонa b, которая равна 6 см. Также нарисованы две диагонали c и d, но их длины неизвестны.

Для нахождения площади этого четырехугольника, мы можем разделить его на два треугольника, используя одну из диагоналей. Нам известно, что площадь треугольника можно найти по формуле:

Площадь треугольника = (основание * высота) / 2.

Поэтому, чтобы найти площадь четырехугольника, мы должны найти площади обоих треугольников и сложить их.

Давай начнем с первого треугольника, который получается путем соединения стороны a с диагональю c. Мы можем найти площадь этого треугольника, используя формулу, которую я только что упомянул.

Так как у нас есть две известные стороны треугольника, a = 8 см и гипотенуза c, мы можем найти третью сторону диагональ d, используя теорему Пифагора:

d² = c² - a²,
d² = c² - 8²,
d² = c² - 64.

Мы не знаем длину диагонали c, поэтому пока обозначим ее как x. Тогда получим:

d² = x² - 64.

Затем, с помощью теоремы Пифагора, мы можем найти длину диагонали d:

d² = x² - 64,
d = √(x² - 64).

Теперь мы можем найти площадь первого треугольника, заменяя a и d в формулу:

Площадь первого треугольника = (a * d) / 2.

Заменяя значения, получим:

Площадь первого треугольника = (8 * √(x² - 64)) / 2
= 4 * √(x² - 64).

Теперь перейдем ко второму треугольнику, который образуется путем соединения стороны b с диагональю d. Аналогично, мы можем найти площадь этого треугольника, используя формулу:

Площадь второго треугольника = (b * d) / 2.

Заменяя значения, получим:

Площадь второго треугольника = (6 * √(x² - 64)) / 2
= 3 * √(x² - 64).

Чтобы найти площадь четырехугольника, мы должны сложить площади обоих треугольников:

Площадь четырехугольника = Площадь первого треугольника + Площадь второго треугольника.

Заменяя значения, получаем:

Площадь четырехугольника = 4 * √(x² - 64) + 3 * √(x² - 64)
= (4 + 3) * √(x² - 64)
= 7 * √(x² - 64).

Таким образом, для нахождения площади четырехугольника, нам необходимо только знать длину диагонали x. Если нам известна эта величина, мы можем подставить ее в формулу и вычислить площадь четырехугольника.

Надеюсь, я смог детально и понятно объяснить, как найти площадь данного четырехугольника! Если у тебя еще остались вопросы или что-то не ясно, пожалуйста, задай их, и я буду рад помочь тебе!