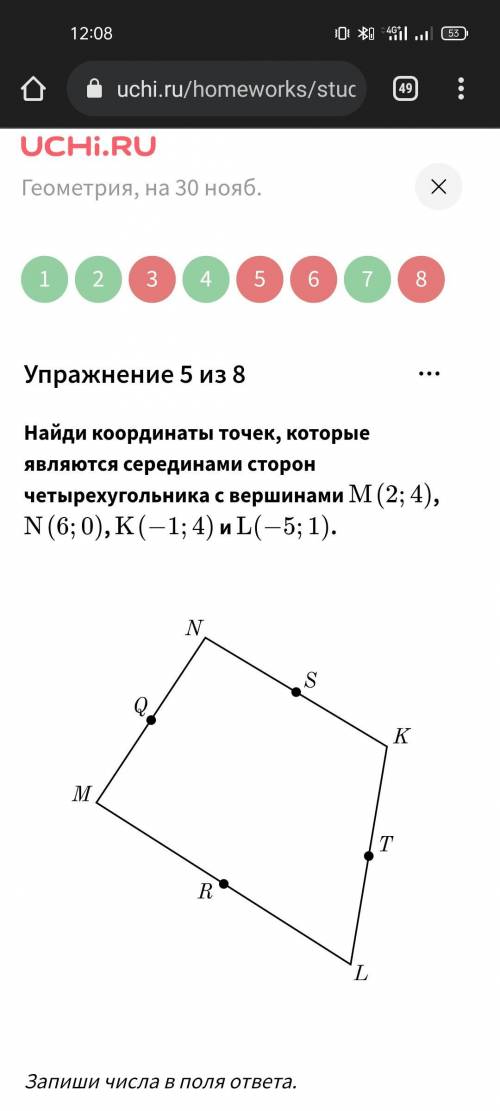
Найди координаты точек, которые являются серединами сторон четырехугольника с вершинами M(2;4)M(2;4) , N(6;0)N(6;0) , K(-1;4)K(−1;4) и L(-5;1)L(−5;1) .

Чтобы найти координаты точек, которые являются серединами сторон четырехугольника, мы можем использовать формулу для нахождения средней точки между двумя данными точками.

Дано, что вершины четырехугольника имеют следующие координаты:
M(2;4), N(6;0), K(-1;4) и L(-5;1).

Первым шагом найдем середину стороны МN.
Для этого мы можем использовать формулу:
середина_стороны_МN = (x_М + x_N)/2, (y_М + y_N)/2

Заменив значения:
середина_стороны_МN = (2 + 6)/2, (4 + 0)/2
середина_стороны_МN = 8/2, 4/2
середина_стороны_МN = 4, 2

Таким образом, координаты середины стороны МN равны (4;2).

Аналогично, мы можем найти середину стороны NK, KL и LM.

Для стороны NK:
середина_стороны_NK = (x_N + x_K)/2, (y_N + y_K)/2
середина_стороны_NK = (6 + (-1))/2, (0 + 4)/2
середина_стороны_NK = 5/2, 4/2
середина_стороны_NK = 2.5, 2

Таким образом, координаты середины стороны NK равны (2.5;2).

Для стороны KL:
середина_стороны_KL = (x_K + x_L)/2, (y_K + y_L)/2
середина_стороны_KL = (-1 + (-5))/2, (4 + 1)/2
середина_стороны_KL = -6/2, 5/2
середина_стороны_KL = -3, 2.5

Таким образом, координаты середины стороны KL равны (-3;2.5).

Для стороны LM:
середина_стороны_LM = (x_L + x_M)/2, (y_L + y_M)/2
середина_стороны_LM = (-5 + 2)/2, (1 + 4)/2
середина_стороны_LM = -3/2, 5/2
середина_стороны_LM = -1.5, 2.5

Таким образом, координаты середины стороны LM равны (-1.5;2.5).

Итак, координаты точек, которые являются серединами сторон четырехугольника, с вершинами M(2;4), N(6;0), K(-1;4) и L(-5;1), равны:
Середина стороны МN: (4;2)
Середина стороны NK: (2.5;2)
Середина стороны KL: (-3;2.5)
Середина стороны LM: (-1.5;2.5)