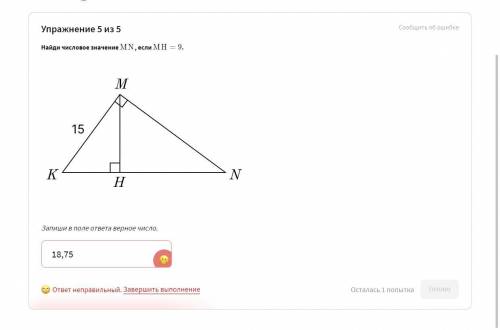
Найди числовое значение MN , если MH = 9 .

Для решения этой задачи нам понадобится использовать теорему Пифагора.

Теорема Пифагора утверждает, что в прямоугольном треугольнике квадрат длины гипотенузы (стороны, противоположной прямому углу) равен сумме квадратов длин катетов (двух остальных сторон).

В данной задаче мы видим прямоугольный треугольник ABC, где гипотенуза — AC, а катеты — AB и BC.

Мы знаем, что MH = 9. Поэтому нам нужно найти длину MN.

Для начала, найдем длины всех сторон треугольника ABC.

AB^2 + BC^2 = AC^2

По условию, AB = 8 и BC = 6.

8^2 + 6^2 = AC^2
64 + 36 = AC^2
100 = AC^2

Теперь найдем длину AC, которая является гипотенузой треугольника ABC.

AC = √100
AC = 10

Теперь, используя теорему Пифагора для треугольника AMN, найдем длину MN.

AM^2 + MN^2 = AN^2

Мы знаем, что AM = AC - CM и CM = CH.

CH = MH = 9 (по условию)
AC = 10 (как мы уже вычислили)

Подставляя известные значения, получаем:

AM = 10 - 9
AM = 1

AN = AC + CN

CN = CH = 9 (так как они вписаны в одну окружность и окружность делит диаметр пополам)

Подставляя известные значения, получаем:

AN = 10 + 9
AN = 19

Теперь мы можем решить уравнение для MN:

AM^2 + MN^2 = AN^2

1^2 + MN^2 = 19^2
1 + MN^2 = 361

MN^2 = 361 - 1
MN^2 = 360

MN = √360
MN = 6√10

Таким образом, числовое значение MN равно 6√10.