1. Геометрия
  2. Напишите каноническое уравнение

Напишите каноническое уравнение эллипса, если фокусное расстояние равно 6, а экс. 3/5

Morikachan46 Morikachan46    3   28.11.2021 20:01    0

Ответы
НЕЗНАЙКА123987 НЕЗНАЙКА123987  05.01.2022 00:24

Напишите каноническое уравнение эллипса, если фокусное расстояние равно 6, а эксцентриситет равен 3/5

Объяснение:

Каноническое уравнение эллипса имеет вид 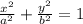  :   \frac{x^{2} }{a^{2} } +\frac{y^{2} }{b^{2} } =1

где a и b (a > b) - длины полуосей.

Тк фокусное расстояние 6 , то с= 3 ;

Тк эксцентриситет ( ε=с/а) равен 3/5 , то а=5. Найдем b из формулы с=√(а²- b²) .

3=√(25-b²) ⇒ b²=25-9 ,b²=16 .  Получаем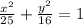  \frac{x^{2} }{25 } +\frac{y^{2} }{16 } =1.

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Геометрия
1goroh2 1goroh2  28.01.2022 21:52
Диагональ треугольника 12 см, угол между диагоналями 30°. Найдите его площадь а ещё можете на листке чертёж+решение написать...
даша3619 даша3619  28.01.2022 21:53
До площини прямокутного ABC кут C = 90 проведений перпендикуляр PB. PA=13см, кут B = 30, AC = 5 см. Знайдіть відстань від точки P а) до прямої AC; б) до площини...
Margarita11mm Margarita11mm  28.01.2022 21:55
Найти периметр шестиугольника ,...
yalex83p0a2c7 yalex83p0a2c7  28.01.2022 21:59
Один із зовнішніх кутів трикутника дорівнює 148°. Знайдіть більший кут трикутника, не суміжний з ним, якщо один з них у 3 рази менший від другого , СДЕЛАЙТЕ С ПОЛНЫМ...
Intagul Intagul  28.01.2022 21:59
Найдите все углы, которые образуются при пересечении двух прямых секущей...
Avetodor Avetodor  28.01.2022 22:04
До площини а з точки А проведено перпендикуляр АС та похилу АБ. Знайти а)БС якщо Аб 10 см. б)АС якщо АБ 10см БС 8 см...
odolskij2016 odolskij2016  28.01.2022 22:05
Постройте в одной координатной плоскости у=х, у=2х, у=3х, у=-х, у=-2х Какой угол образуют эти графики с осью ОХ? В каких четвертях расположены графики? Сделайте...
sadgirl22 sadgirl22  28.01.2022 22:05
с задачейдан параллелограмм ABCDBE=4 смугол А=45°Найти: CD...
joje1 joje1  01.10.2019 21:20
Точки a(-6; 7) и b(4; 5) - концы диаметра окружности.составьте уравнение этой окружности и прямой,проходящей через её центр и параллельной оси абсцисс / параллельной...
Denistypitjin Denistypitjin  01.10.2019 21:20
Треугольник abc задан координатами своих вершин a(-6; 1), b(2; 4), c(2; -2). а) докажите,что треугольник abc - равнобедренный. б) найдите высоту,проведённую к основанию...

Популярные вопросы