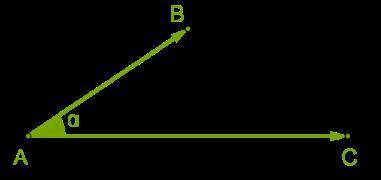
На точку A действуют две силы величиной ∣∣∣AB−→−∣∣∣=22N и ∣∣∣AC−→−∣∣∣=68N, угол между ними — ∡A=50°. Определи величину силы, которая в результате действует на точку A (округли результат до целых).
Другие вопросы по теме Геометрия
Популярные вопросы
- Пользуясь рисунком 11,б, определите погрешность измерения термометра?...
3 - До поданих слів добрати синонімом 1) сумувати2)їжа3) відважний4) горизонт...
2 - Можете решите,определения не надо) 50...
1 - 11, ,распишите подробнее почему так...
1 - Паскаль. определить средний одного ученика с массива или цикла с предусловием...
3 - Твір роздум чому більшість неологізмів у мові-іншомовні слова...
1 - На доске написаны числа от 1 до 100. за один ход стираются 2 числа, а...
1 - Назовите семейные праздники в россии и что в этом празднике...
2 - 13 . почему ахмет байтурсынов считал, что существование казахского народа...
2 - Из данных чисел: 12,131,11,10 составь верную запись деления с остатком....
2
1) Разобьем силы AB и AC на составляющие по осям X и Y. Для этого умножим величины сил на cos и sin их угла относительно оси X соответственно.
Для силы AB:
ABx = AB * cos(50°)
= 22 * cos(50°)
≈ 14.10 N
ABy = AB * sin(50°)
= 22 * sin(50°)
≈ 16.87 N
Для силы AC:
ACx = AC * cos(180°-50°)
= AC * cos(130°)
= 68 * cos(130°)
≈ -34.00 N (отрицательное значение, так как сила направлена влево по оси X)
ACy = AC * sin(180°-50°)
= AC * sin(130°)
= 68 * sin(130°)
≈ 59.82 N
2) Теперь сложим составляющие по каждой оси, чтобы получить результирующую силу.
Результирующая сила по оси X:
Rx = ABx + ACx
= 14.10 N + (-34.00 N)
≈ -19.90 N
Результирующая сила по оси Y:
Ry = ABy + ACy
= 16.87 N + 59.82 N
≈ 76.69 N
3) Найдем величину результирующей силы R, используя теорему Пифагора:
R = √(Rx^2 + Ry^2)
= √((-19.90 N)^2 + (76.69 N)^2)
≈ √(396.01 N^2 + 5883.76 N^2)
≈ √(6280.77 N^2)
≈ 79.25 N (округляем до целого)
Таким образом, величина силы, которая в результате действует на точку A, составляет примерно 79 Н.