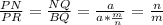На стороне pq треугольника pqr взята точка n, а на стороне pr – точка l, причем nq = lr. точка пересечения отрезков ql и nr делит отрезок ql в отношении m: n, считая от точки q. найдите отношение pn: pr.
Другие вопросы по теме Геометрия
Популярные вопросы
- Какае два существа внесли в жизнь герасима радость,как он заними ухаживал...
1 - 5предложений с деепричастным оборотом из художественной ....
2 - Какие отрасли животноводство особенно развиты в алтайском крае!...
1 - Найдите : а) 60% от 12 кг ; б) 25% от 40дм...
1 - Составьте сочинение 2-3 предложения на . тема: мои проблемы ( только не про...
3 - Подробно x^4 + x^2 + 1 x^3 - 3*x + 2...
2 - Проверьте на наличие ошибок в пунктуации и словах! ) у каждого человека своя...
2 - Окаких частях речи нельзя сказать, что они изменяются по числам и ? а)имя существительных...
2 - Диалогті толықтырып, өзара сқйлесіңдер (составьте вопросы). 1) - - бағзы замандарда...
1 - Уприставки со нет значение вместе в слове. сотрудник соавтор собеседник соврать...
3
Объяснение:
Пусть QL и NR пересекаются в одной точке - A.
NQ=LR=a
Через точку Q проведём прямую, которая параллельна PR. Пусть эта прямая будет пересекаться с прямой NR в точке B. Из подобия треугольников BAQ и RAL следует, что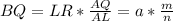
Из этого подобия треугольников BNQ и RNP находим, что