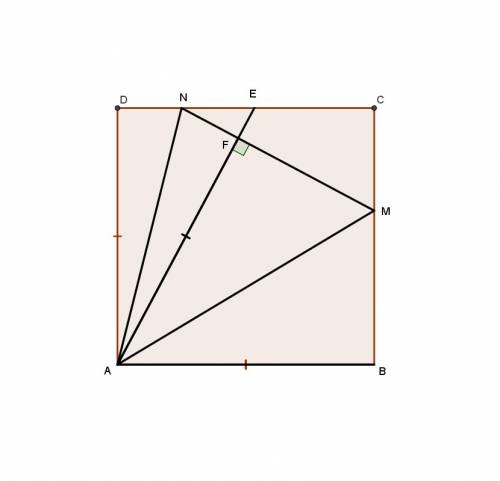
На стороне cd квадрата abcd отмечена точка e. биссектрисы углов eab и ead пересекают стороны bc и cd в точках m и n соответственно. на луче ae отмечена такая точка f, что af = ab. докажите, что f лежит на прямой mn.
Ответы
ΔADN=ΔAFN по 1 признаку (AF=AB=AD, AN - общая, ∠DAN=∠FAN т.к. AN - биссектриса). Значит ∠AFN=∠ADN=90°. Аналогично, ΔBAM=ΔFAM, откуда ∠AFM=∠ABM=90°. Т.е. ∠AFM+∠AFN=180°, т.е. F лежит на MN.
ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Геометрия
Популярные вопросы
- Какие гормоны действуют на яичник,остеон, нефрон?...
2 - Прямоугольный газон обнесен изгородью , длина которой 30м. площадь...
2 - Сколько сгорело этона, если образовалось 18 г воды ?...
2 - Составить письмо другу про зож , с советами и рекомендациями как...
1 - Ниже перечень терминов, названий. все они, за исключением одного,...
2 - Завтра экзамен! по уравнению hgo-hg-o2-42кдж рассчитать,сколько...
2 - Впервом букете было в 4 раза меньше роз чем во втором когда спирохета...
1 - Втрех пронумерованных пробирках находятся фенол, уксусный альдегид...
1 - навстречу на это слово словообразовательный разбор, именно как...
3 - Перевести на . 2. если я не экзамен, я буду учить предмет. 3. как...
3