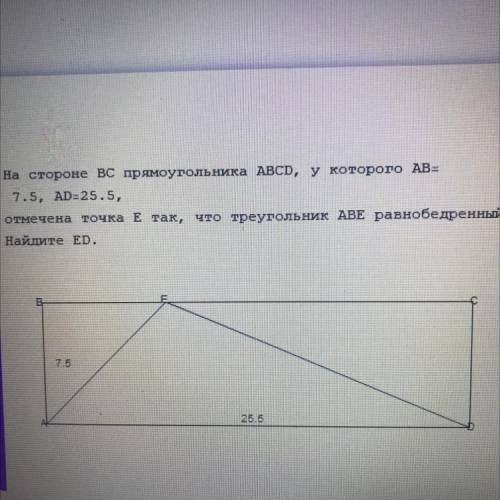
На стороне BC прямоугольника ABCD, у которого AB= 7.5, AD=25.5,
отмечена точка E так, что треугольник ABE равнобедренный.
Найдите ED.

25.5

Чтобы найти ED, нам сначала нужно понять, какие свойства имеет равнобедренный треугольник ABE. В равнобедренном треугольнике две стороны равны между собой, а углы противоположные им равны. В данном случае, AB = AE, так как треугольник ABE - равнобедренный.

Теперь мы можем воспользоваться этим свойством, чтобы найти значение ED. Для этого нужно вычислить длину стороны AE с использованием теоремы Пифагора.

Из прямоугольника ABCD известно, что AD = 25.5 и AB = 7.5. Тогда, по теореме Пифагора, можно найти длину стороны AC:

AC^2 = AD^2 + AB^2
AC^2 = 25.5^2 + 7.5^2
AC^2 = 650.25 + 56.25
AC^2 = 706.5

Затем, поскольку треугольник ABE равнобедренный и AB = AE, мы можем записать:

AC = AE + EC

Теперь мы можем использовать значение AC, чтобы выразить EC. Заменив AC на его выражение AE + EC, получим:

AE + EC = √(706.5)

Теперь нужно выразить EC, чтобы найти ED. Для этого нужно использовать равенство сторон треугольника АСЕ:

AB + BE = AC

Замещаем AB на его значение 7.5, AE на его значение AE и AC на его выражение AE + EC, получаем:

7.5 + BE = AE + EC

Также мы знаем, что BE = EC (так как треугольник равнобедренный), поэтому можем заменить BE на EC:

7.5 + EC = AE + EC

Затем EC уходит, и мы получаем:

7.5 = AE

Таким образом, AE = 7.5.

Теперь мы можем использовать это значение, чтобы выразить EC:

AE + EC = √(706.5)
7.5 + EC = √(706.5)
EC = √(706.5) - 7.5

Теперь мы можем подставить полученное значение EC в выражение для ED:

ED = EC
ED = √(706.5) - 7.5

Таким образом, ED равно √(706.5) - 7.5.